Resolva pelo método da adição:
Passo 1
A ideia do método da adição é você somar as duas equações e zerar ou sumir com uma das incógnitas. Vamos primeiro escolher uma incógnita para zerar, pode ser a . Agora, precisamos pensar em um número para multiplicar a primeira equação, para que na hora que somarmos com a segunda a variável zere. Olhando para a segunda equação:
Temos um , para zerar preccismos soma-lo com um porém na primeira equação temos apenas . Assim, podemos multiplicar nossa primeira equação por , e somar com a segunda.
Passo 2
Fazendo a multiplicação por :
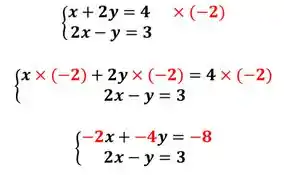
Feito isso, vamos somar as duas equações:
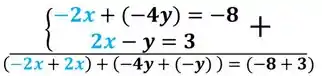
Resolvendo a equação :
Passo 3
Agora que descobrimos o valor de y, vamos voltar em uma das equações iniciais e substituir, vamos pegar a segunda equação:
Substituindo:
Assim, o par ordenado , é solução do nosso sistema.
Resposta
O que é o mesmo que: