Com o auxílio da tabela calcule a rigidez e a rigidez específica da barra nos nós e . Sabendo que e .
Passo 1
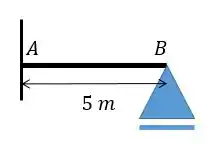
Faaala, galerinha!!! Aqui temos um exercício com uma viga simples engastada no lado e apoiada no lado e queremos achar a rigidez e a rigidez específica . Lembrando que a relação entre as duas é:
Outra coisa que a gente deve lembrar é que tanto o apoio de primeiro quanto segundo gênero estão suscetíveis à rotação, dessa forma pode-se falar que o lado apoiado está rotulado.
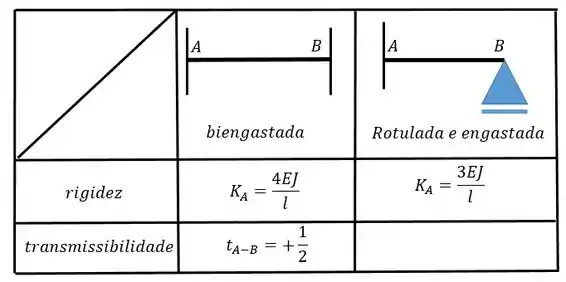
Agora é olhar para a tabela e resolver o probleminha que é bem direto. Vamos fazer isso juntos nos próximos passos =D
Passo 2
Quando a gente olha o nosso problema e a nossa tabela a gente percebe que só existe uma possibilidade de rigidez para o nó (não é mesmo? A barra está engastada e apoiada) então vamos ter:
Agora é só substituir os valores:
Mas podemos escrever com uma forma mais usual:
Que belezaaa.
Passo 3
Agora podemos calcular a rigidez específica da barra em .
Substituindo:
Passo 4
Para a barra nós vamos ter que a rigidez é nula. Isso acontece porque o nó não resiste à rotação. Então:
Por isso que a tabela não fornece o valor do coeficiente de transmissibilidade para o nó , porque na real esse coeficiente é igual a zero!