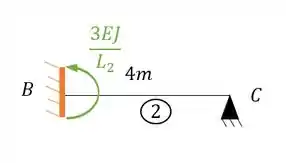
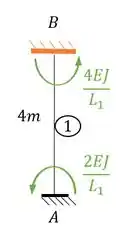
para o pórtico abaixo represente cada trecho como uma viga separada e determine as rigidezes que podem aparecer para cada um dos trechos analisados.
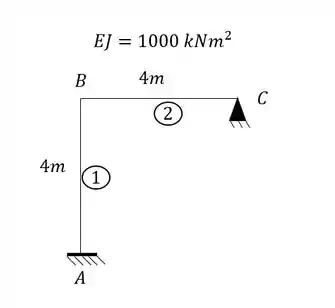
Passo 1
Como vimos na teoria, o que está ligado a cada uma das deslocabilidades segue o seguinte padrão:
- Para deslocabilidades internas usamos as rigidezes voltadas para rotação
- Para deslocabilidade externas usamos as rigidezes voltadas para deslocamento
Sendo assim teremos que determinar primeiro o tipo de deslocabilidades que temos na nossa viga.
Passo 2
Vamos analisar primeiro as deslocabilidades ligadas a cada um dos apoios:
- Apoio A e C
- Apoio B
- Total de deslocabilidades
- Temos uma viga do tipo engastada e apoiada
- O tipo de deslocabilidade dela é interna (ou seja, ligada a rotação)
- Trecho horizontal
- Perceba que temos uma viga do tipo Bi-engastada
- Os tipos de deslocabilidades dela são internas (ou seja, ligada a rotação)
- Trecho vertical
Os apoios A e C são apoio do tipo engaste, logo não possuem nem deslocabilidade interna e nem deslocabilidade externa.
O apoio B está ligado aos engastes da base, que são indeslocaveis, logo o nó B não possui deslocabilidade externa, porém veja que ele pode rotacionar, dessa forma, identificamos que o nó possui deslocabilidade interna, sendo nesse caso, contabilizado, uma deslocabilidade interna.
Passo 3
Tendo isso precisamos agora separar o nosso pórtico, e para isso quebramos apenas a deslocabilidade interna que foi contabilizada:
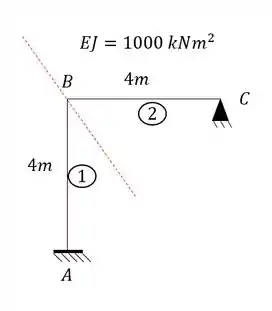
Perceba que se rompêssemos o nosso pórtico no apoio B, teríamos valores de reação vertical, horizontal e de momentos fletores, ou seja, nosso nó B seria a representação de um engaste, que poderíamos agrupar como:
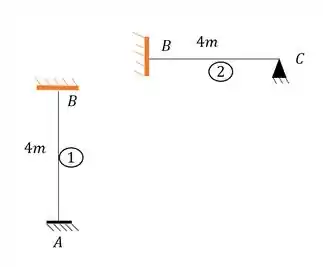
Passo 4
Agora já fizemos o mais difícil, quando chegarmos na aula do passo a passo de método das deslocabilidades vamos ver que não há necessidade de ficarmos dividindo toda a nossa estrutura, mas estamos fazendo isso aqui para deixar bem claro o porque de usarmos certas fórmulas ao invés de outras, então pode estar dando um trabalhinho agora, mas depois vai ficar mais tranquilo:
Sendo assim, olhando o nosso desenho, só precisamos determinar a nossa fórmula, com isso basta listarmos o que temos, que é:
Logo a fórmula que devemos usar é essa aqui
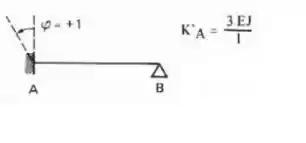
Aplicando a nossa viga teremos que:
Vamos gira-la sempre no sentido anti-horário para podermos ter as rigidezes sempre positivas, sendo assim teremos que:
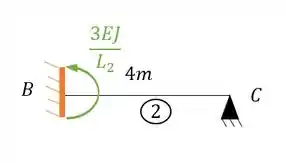
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Logo a fórmula que devemos usar é essa aqui
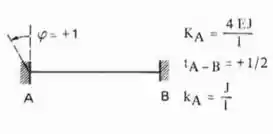
Aplicando a nossa viga, teremos:
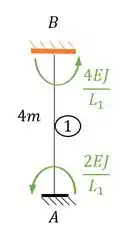
Substituindo teremos que:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva mesmo, sendo assim teremos que:
Perceba que temos também o ponto A, logo:
Perceba que nesse caso a nossa rigidez está no sentido anti-horário, logo a nossa representação correta deve ser positiva, sendo assim teremos que:
Resposta