Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Rigidez de um nó de uma viga

Ver Teoria
Exercício 71234568

Enunciado

Com o auxílio da tabela calcule a rigidez e a rigidez específica do nó B . Sabendo que E = 200   G P a e J = 10 - 5   m 4 .

Passo 1

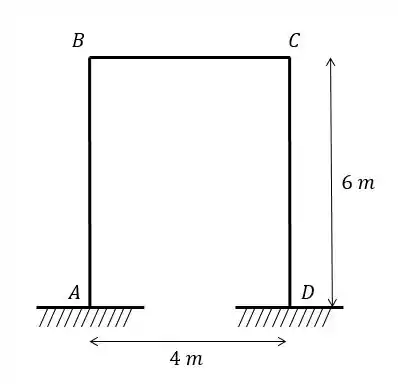
Faaala, galerinha!!! Aqui temos um exercício com um pórtico engastado nas bases e queremos achar a rigidez K e a rigidez específica k do nó B . Lembrando que a relação entre as duas é:

k = K 4 E

Para resolver esse exercício vamos olhar na tabela e descobrir qual melhor equação utilizar, mas para isso nós precisamos dividir as barras corretamente. O que consiste em saber onde estão os pontos sujeitos à rotação.

Passo 2

Os nós que estão sujeitos à rotação são os nós B e C , logo esses nós são separados da nossa estrutura e substituídos por engastes:

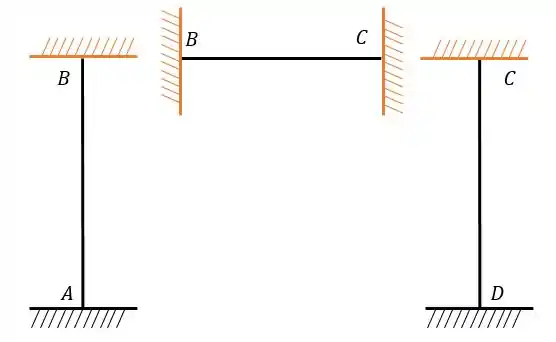
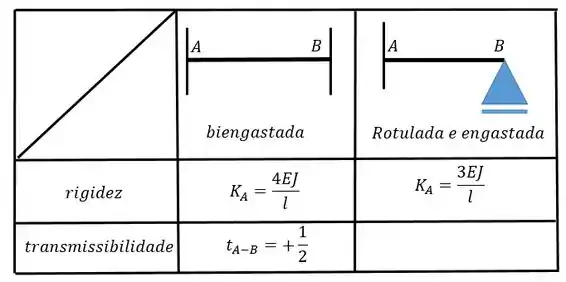
Perceba que a gente vai tratar o nosso pórtico como três barras distintas, como queremos apenas as grandezas referentes ao nó B vamos olhar para as barras A B e B C . Ambas são biengastadas, logo nossa equação será:

K = 4 E J l

Fazendo para a barra A B vamos ter:

K B = 4 200.10 9 ( 10 - 5 ) 6 = 1,33.10 6   N . m

Mas podemos escrever com uma forma mais usual:

K B = 1,33.10 3   k N m

E para a barra A C vamos ter:

K B ' = 4 200.10 9 ( 10 - 5 ) 4 = 2,0.10 6   N . m

Mas podemos escrever com uma forma mais usual:

K ' B = 2,0.10 3   k N m

Passo 3

Agora podemos calcular a rigidez específica. Para a barra A B :

k B = K B 4 E

Substituindo:

k B = 1,33.10 6   N . m 4 200.10 9 N / m 2

k B = 1,67.10 - 6   m 3

Para a barra B C :

k ' B = K ' B 4 E

Substituindo:

k ' B = 2,0.10 6   N . m 4 200.10 9 N / m 2

k ' B = 2,5.10 - 5   m 3

Resposta

Para a barra A B :

K B = 1,33.10 3   k N m

k B = 1,67.10 - 6   m 3

Para a barra B C :

K ' B = 2,0.10 3   k N m

k ' B = 2,5.10 - 5   m 3