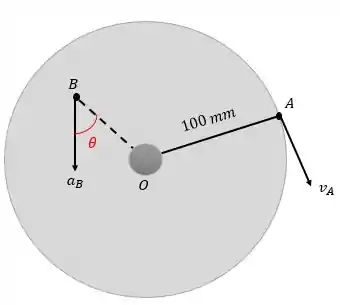
O disco circular gira em torno de seu centro . Em um determinado instante o ponto possui uma velocidade na direção mostrada, e no mesmo instante a tangente do ângulo dado pelo vetor aceleração total de um ponto qualquer com sua linha radial até é de 0,6. Calcule para esse instante a aceleração angular do disco.
Passo 1
A aceleração de um ponto que pertence a um corpo rígido que esteja realizando rotação, pode possuir duas componentes: uma tangencial e outra centrípeta.
A componente tangencial é tangente à trajetória e aponta na direção do movimento do disco:
E a componente normal é perpendicular à trajetória aponta para o centro do disco:
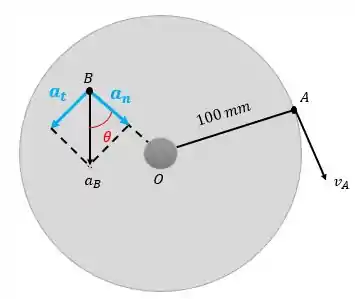
Passo 2
Precisamos achar a velocidade angular do disco. Para isso, vamos usar a informação sobre o ponto .
O ponto tem um velocidade e sabemos que a velocidade de um ponto que pertence a um corpo rígido em rotação é:
Então:
Repare que a velocidade angular é negativa, pois faz o disco girar no sentido horário.
Então, já podemos calcular a componente normal da aceleração do ponto:
Por enquanto vamos deixar em função do raio, pois não sabemos seu valor.
Passo 3
Agora vamos calcular a aceleração angular. Para isso, temos que usar a informação de que a tangente do ângulo dado pelo vetor aceleração total de um ponto qualquer com sua linha radial até é de 0,6:
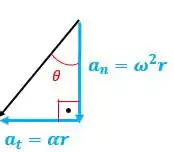
Como já sabemos que , então: