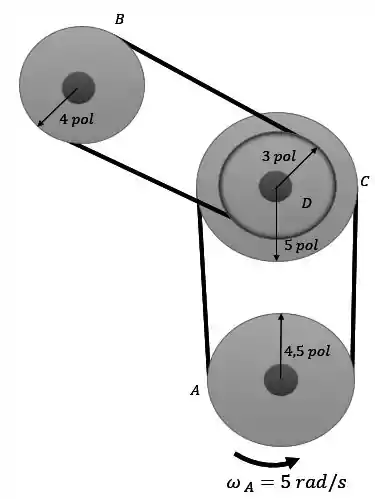
Um moinho usa um arranjo de polias e correias para transmissão de potência. Quando , um motor elétrico está girando a polia com velocidade angular . Se a polia está sujeita a uma aceleração angular de , determine a velocidade angular da polia após esta ter executado 6 revoluções. O cubo em está rigidamente conectado à polia , girando com ela.
Passo 1
Nesse exercício temos que trabalhar com as fómulas de transmissão de movimento entre as polias, tanto de velocidade angular:
Quanto de aceleração angular:
A polia possui uma velocidade angular inicial de , então vamos ir transmitindo isso para as outras polias até acharmos a velocidade angular inicial da polia .
Repare que a polia está conectada à polia , então:
Observe que a polia está conectado com a polia , girando com ela. Então, a polia realiza os mesmos movimentos que a polia :
Agora repare que a polia está conectada pela corda com a polia , então vamos ter que:
Opa, já temos a velocidade da polia quando !
Passo 2
Nosso próximo passo é trabalhar com a aceleração. Como a polia foi submetida a uma aceleração angular constante, quando ela for transmitindo seu movimento, cada polia terá sua própria velocidade angular constante.
A polia está conectada com a polia , então vamos ter que:
Como vimos antes, a polia está conectada rigidamente à polia , logo todo movimento que faz, a polia também vai fazer. Então:
Como a polia está ligada à polia , a sua aceleração será:
Essa é a aceleração angular da polia e ela é constante assim como a aceleração angular da polia também é constante.
Passo 3
Agora temos que calcular a velocidade angular final da polia após ela ter dado 6 revoluções.
Para isso temos que saber que:
Então, para 6 revoluções teremos:
Esse é o deslocamento angular da polia .
Como a aceleração angular é constante, temos que procurar uma equação que relacione velocidade angular e deslocamento angular:
O deslocamento inicial ()da polia é zero, então: