O volante possui um diâmetro de e gira com uma velocidade cada vez maior em torno de sua árvore no eixo . Quando o ponto sobre a borda cruza o eixo com , possui uma aceleração dada por . Para esse instante, determine a velocidade angular e a aceleração angular do volante.
Passo 1
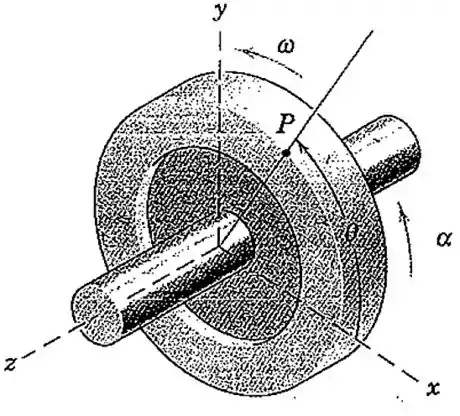
Primeiro vamos entender o que está acontecendo. O volante está girando com uma velocidade que está crescendo, logo ele tem uma aceleração com duas componentes. Quando o ponto tem um ângulo de , ele possui essa aceleração aqui:
Que pode ser escrita nas suas componentes e :
Então, vamos ter os seguintes vetores:
Passo 2
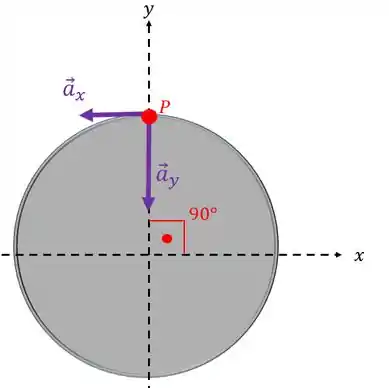
Agora vamos achar a velocidade angular do volante. Para isso, vamos usar a componente centrípeta da aceleração ().
A aceleração centrípeta sempre aponta para o centro da curva, então ela será equivalente ao nosso vetor .
Lembra como se calcula a aceleração centrípeta?
Opa, olha quem apareceu aí. É justamente a velocidade angular que queremos saber. Já sabemos que e . Agora é só alegria:
Então:
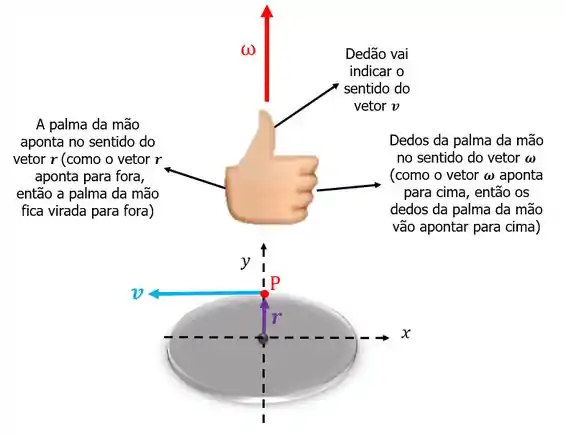
E o sentido da velocidade angular? É só usar a regra da mão direita:
Passo 3
Repare que a velocidade varia no tempo, portanto a aceleração tem componente tangencial que é responsável pela mudança do módulo da velocidade. A componente tangencial é aquele vetor que tangencia a curva, certo? Então vamos ter:
E como se calcula a aceleração tangencial mesmo? É assim né:
O raio nós sabemos que é e a aceleração tangencial nós também conhecemos que é . Então, podemos achar a aceleração angular do volante:
Não usei o sinal, porque estamos calculando o módulo. E quanto ao sentido da aceleração angular? Ela terá o mesmo sentido do vetor velocidade angular , porque está aumentando. Ou seja, aponta no sentido positivo do eixo .