Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Rotação de Corpos Rígidos

Ver Teoria
Exercício 1234567

Enunciado

Um motor gira uma engranagem A com aceleração α A = 0,25 θ 3 + 0,5   r a d / s 2 , onde θ é dado em radianos. Se A tem velocidade angular inicial ( ω A ) 0 = 20   r a d / s , determine a velocidade angular da engrenagem B após A ter sofrido um deslocamento angular de 10   r e v .

Dados: r A = 0,05   m e r B = 0,15   m .

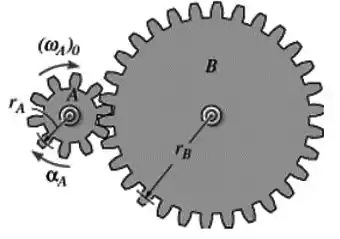
Passo 1

Nós temos uma aceleração da engrenagem A que varia com o deslocamento angular θ e temos a velocidade angular inicial desta mesma engrenagem. Que equação relaciona essas duas grandezas?

α d θ = ω d ω

Vamos ter que integrar de ambos os lados, sabendo que α A = 0,25 θ 3 + 0,5 :

α d θ = ω d ω         →           ∫ ( 0,25 θ 3 + 0,5 ) d θ = ∫ ω d ω

Qual será o nosso intervalo de integração? Sabemos que o deslocamento angular da engrenagem A é de 10   r e v o l u ç õ e s . Para converter revolução para radianos, temos que saber que:

1   r e v = 2 π   r a d

Então, 10   r e v terá:

10   r e v = 10 2 π   r a d       →             10   r e v = 20 π   r a d

Já temos um intervalo de integração:

∫ 0 20 π ( 0,25 θ 3 + 0,5 ) d θ = ∫ ω d ω

E para a velocidade angular, temos a informação que a velocidade angular inicial da engrenagem A é de ( ω A ) 0 = 20   r a d / s . Já a sua velocidade angular final é o que queremos saber, pois é através dela que iremos calcular a velocidade da outra engrenagem.

∫ 0 20 π ( 0,25 θ 3 + 0,5 ) d θ = ∫   ( ω A ) 0   ( ω A ) f ω d ω

Agora é só integrar:

∫ 0 20 π ( 0,25 θ 3 + 0,5 ) d θ = ∫   ( ω A ) 0 = 20   ( ω A ) f ω d ω         →             0,25 θ 4 4 + 0,5 θ | 0 20 π = ω 2 2 | 20 ( ω A ) f

Substituindo os valores teremos:

0,25 ( 20 π ) 4 4 + 0,5 ( 20 π ) = ( ω A ) f 2 - 20 2 2

0,25 ( 20 π ) 4 4 + 0,5 ( 20 π ) 2 + 20 2 = ( ω A ) f 2

( ω A ) f = 1948244,65 + 400

( ω A ) f = 1395,94     r a d / s

Passo 2

Agora temos que lembrar da relação que temos entre a transmissão de movimento entre duas polias ou engrenagens:

ω A r A =   ω B r B

Então, a velocidade angular da engrenagem B será:

  ω B = ω A r A r B

Temos que r A = 0,05   m e r B = 0,15   m , então:

ω B = 1395,94   ( 0,05 ) 0,15

ω B = 465,3   r a d / s

Resposta

ω B = 465,3   r a d / s

Exercícios de Livros Relacionados

54. O pinhão A roda sobre a cremalheira fixa B com uma velocidade angular ω = 4 r a d s . Determine a velocidade da cremalheira C.