A placa forma um triângulo equilátero que gira no sentido anti-horário com velocidade crescente em torno do ponto . Se as componentes normal e tangencial da aceleração do centróide em um determinado instante são e , respectivamente, determine os valores de e nesse mesmo instante. O ângulo é o ângulo entre a linha e o eixo horizontal fixo.
Passo 1
Primeiro vamos posicionar as coordenadas normal e tangencial () no centróide da peça:
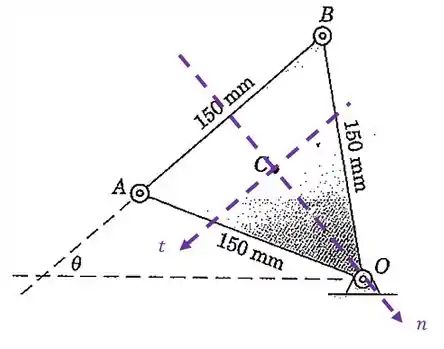
Não esqueça que o eixo aponta no sentido do movimento (anti-horário) e o eixo aponta para o centro da curva que o movimento faz. Ou seja, como o corpo gira em torno do ponto , o eixo aponta para este ponto.
Vamos colocar agora os vetores aceleração que foi dado no enunciado:
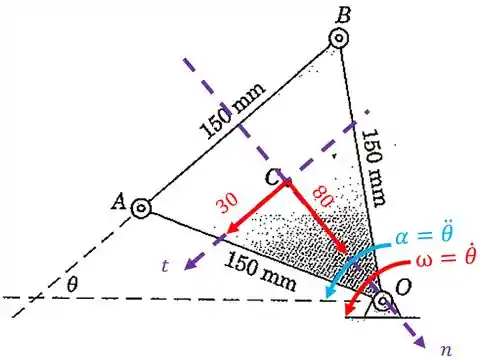
Lembra que a velocidade angular também pode ser chamada de e a aceleração angular também pode ser representada por . É justamente isso que o enunciado faz! ![]()
A aceleração tem duas componentes: uma tangencial à trajetória (aceleração tangencial) e outra normal à trajetória circular (aceleração centrípeta):
Lembra a fórmula da aceleração centrípeta?
Vamos usar esta fórmula para achar a velocidade angular do centróide. Mas para isso temos que achar o raio da trajetória circular que o centróide faz. Vamos ter o seguinte círculo:
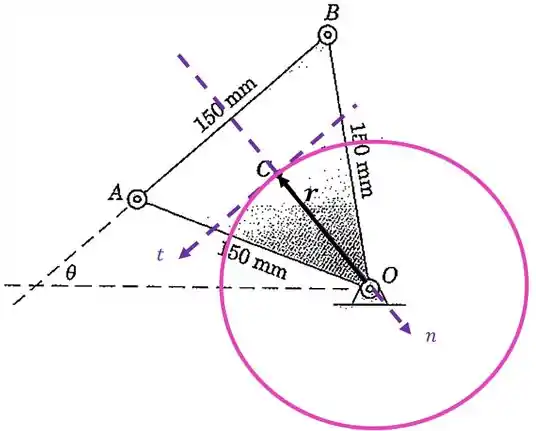
Passo 2
Vamos ter que lembrar de como é um triângulo equilátero para calcular o raio :
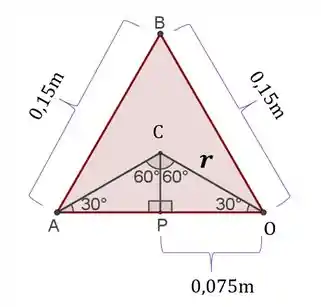
Para calcular o raio vamos usar o seguinte triângulo:
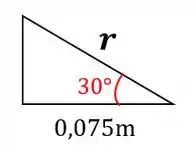
Agora podemos calcular a velocidade angular do ponto :
Podemos escrever também:
Passo 3
Nosso próximo passo é calcular a aceleração angular do ponto . Para isso, vamos usar a equação da aceleração tangencial:
Sabemos que e , então: