A velocidade angular do disco é definida por , onde é dado em segundos. Determine os módulos da a) velocidade e b) aceleração do ponto do disco quando .
Passo 1
Para determinar a velocidade do ponto que pertence ao disco que está girando, usamos a seguinte fórmula:
Repare que para achar temos que determinar o valor de antes usando a equação que foi dado no enunciado:
Para o tempo :
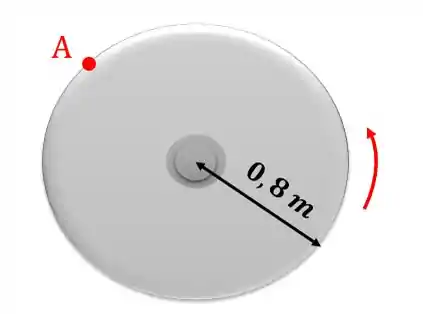
Sabendo pela figura que o raio , agora sim podemos achar a velocidade do ponto A:
Passo 2
Nosso próximo passo é determinar a aceleração. Não podemos esquecer que a aceleração tem duas componentes, uma tangencial e outra normal:
Vamos achar a componente tangencial primeiro. Para isso, temos que determinar a aceleração angular :
Como , então:
Para o tempo , vamos ter o seguinte valor de aceleração:
Agora é só acharmos a aceleração tangencial:
Passo 3
Agora vamos achar a aceleração normal que é:
Nós já sabemos o valor de quando , pois já achamos isso no passo 1.
Então é só substituir:
Beleza! Como a questão pediu o módulo da aceleração é só aplicarmos o teorema de Pitágoras para achar a aceleração resultante: