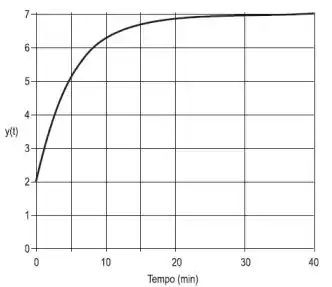
A figura abaixo representa a resposta da variável de saída a uma perturbação degrau de magnitude de unidades na variável de entrada de um processo, a partir de um instante em que o processo estava em regime permanente. Com base nessas informações defina a função de transferência do processo.
Passo 1
O exercício pede que a gente determine a função de transferência do processo, e pela cara do gráfico já dá pra matar que é uma função de transferência de primeira ordem.
A função de transferência de primeira ordem padrão é desse jeitinho aqui ó:
Então, para determinar nossa F.T. devemos encontrar os valores dos parâmentros e .
Passo 2
Vamos focar primeiramente no nosso ganho .
O ganho, por definição é a razão entre a variação da variável de saída sobre a variação da variável de entrada.
Pelo nosso gráfico podemos ver que a variável de saída vai de até , e o enunciado nos diz que a variação na entrada foi de magnitude . Então:
Passo 3
Vamos partir então para a determinação da nossa contante de tempo .
Uma das propriedades das constantes de tempos em funções de transferência de primeira ordem, é que quando , resposta se encontra em aproximadamente da variação total.
Então para encontrar o nosso precisamos encontrar o tempo em que:
Esse valor de é atingido quando , sendo assim: