Obtenha a resposta de saída, , para cada um dos sistemas mostrados abaixo. Além disso, obtenha a constante de tempo, o tempo de subida e o tempo de acomodação para uma faixa menor que da resposta final para cada caso.
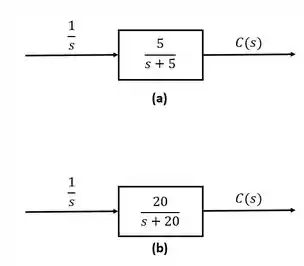
Passo 1
Esse é aquele tipo clássico de questão onde a gente tem uma função de transferência e precisamos compará-la com a função de transferência padrão para encontrar nossos parâmetros.
A função de transferência padrão de primeira ordem é assim:
Precisamos então colocar a nossa função de transferência nessa forma. Para isso, o termo independente de s no denominador precisa ser 1. Então dividimos nossa função de transferência em cima e embaixo por ele. Para o item (a):
Passo 2
Agora já podemos fazer a comparação. No item (a):
Agora que temos nossa constante de tempo, , podemos calcular o tempo de subida, , e o tempo de acomodação, .
Passo 3
Para encontrar a resposta devemos calcular a transformada de Laplace inversa de
Porém, a gente já tem um modelinho pronto pra funções de primeira ordem com entrada degrau:
Então, só precisamos substituir os valores de ganho, constante de tempo e de amplitude do degrau na equação:
Passo 4
Fazendo o mesmo para o item (b)
Comparando com a equação padrão:
Passo 5
Os tempos de subida e acomodação serão:
E a resposta :
Resposta
Ei, a resposta está no passo a passo :)