Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Spline Cúbica Interpolante

Ver Teoria
Exercício 123

Enunciado

Construa a spline cúbica natural para as seguintes tabelas:

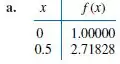
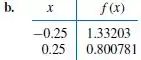
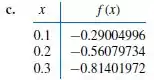
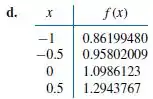
Passo 1

a Primeiro definimos:

x 0 = 0 ; x 1 = 0.5

h 1 = 0.5

Substituindo no nosso sistema A x = b :

A = 1 0 0 1

b = 0 0

Repare que como a primeira e última linha de A e de b devem ser zeradas a gente acaba não tendo que fazer conta nenhuma haha.

Resolvendo isso aí temos:

b 0 = 0

b 1 = 0

Jogando na fórmula:

a 1 = b 1 - b 0 3 h 1 = 0

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = 2.71828 - 1 0.5 = 3.43656

d 1 = f x 1 = 2.71828

Passo 2

Como só temos um intervalo então nossa função será:

S 3 x = s 1 x = 3.43656 x - 0.5 + 2.71828

s 1 x = 1 + 3.43656 x ,   x ∈ 0,0.5

Passo 3

b Definimos:

x 0 = - 0.25 ; x 1 = 0.25

h 1 = 0.5

Substituindo no nosso sistema A x = b :

A = 1 0 0 1

b = 0 0

Resolvendo isso aí temos:

b 0 = 0

b 1 = 0

Jogando na fórmula:

a 1 = b 1 - b 0 3 h 1 = 0

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = 0.800781 - 1.33203 0.5 = - 1.0625

d 1 = f x 1 = 0.800781

Passo 4

Como só temos um intervalo então nossa função será:

S 3 x = s 1 x = - 1.0625 x - 0.25 + 0.800781

s 1 x = 1.06641 - 1.0625 x ,   x ∈ - 0.25,0.25

Passo 5

c Definimos:

x 0 = 0.1 ; x 1 = 0.2 ; x 2 = 0.3

h 1 = h 2 = h = 0 . 1

Substituindo no nosso sistema A x = b :

A = 1 0 0 h 1 2 h 1 + h 2 h 2 0 0 1 = 1 0 0 0.1 0.4 0.1 0 0 1

b = 0 f x 2 - f x 1 h 2 - f x 1 - f x 0 h 1 0 = 0 0.52575 0

Resolvendo isso aí temos:

b 0 = 0

b 1 = 1.314375

b 2 = 0

Passo 6

Aqui temos dois intervalos. Jogando na fórmula do primeiro:

a 1 = b 1 - b 0 3 h 1 = 4.38125

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = - 2.6198488

d 1 = f x 1 = - 0.56079734

E para o segundo intervalo:

a 2 = b 2 - b 1 3 h 2 = - 4.38125

c 2 = f x 2 - f x 1 h 2 + h 2 2 b 2 + b 1 3 = - 2.4884113

d 2 = f x 2 = - 0.81401972

Passo 7

Juntando tudo:

S 3 x = s 1 x = 4.38125 x - 0.2 3 + 1.3144 x - 0.2 2 - 2.6198 x - 0.2 - 0.5608 ,       x ∈ 0.1,0.2 s 2 x = - 4.38125 x - 0.3 3 - 2.4884 x - 0.3 - 0.814 ,       x ∈ 0.2,0.3

Passo 8

d Força agora que estamos na última letra! Nessa temos:

x 0 = - 1 ; x 1 = - 0.5 ; x 2 = 0 ; x 3 = 0.5

E todos os h são iguais de novo (para nossa alegria):

h = 0.5

Agora fazemos o de sempre. Substituímos no sistema A x = b :p

A = 1 0 0 0 h 1 2 h 1 + h 2 h 2 0 0 h 2 2 h 2 + h 3 h 3 0 0 0 1 = 1 0 0 0 0.5 2 0.5 0 0 0.5 2 0.5 0 0 0 1

b = 0 f x 2 - f x 1 h 2 - f x 1 - f x 0 h 1 f x 4 - f x 3 h 4 - f x 3 - f x 2 h 3 0 = 0 0.2674 0.33103 0

Resolvendo o sistema chegamos a:

b 0 b 1 b 2 b 3 = 0 0.098476 0.140897 0

Passo 9

Esse vai ser mais chatinho porque tem 3 intervalos. Pro primeiro intervalo temos:

a 1 = b 1 - b 0 3 h 1 = 0.06565

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = 0.22488

d 1 = f x 1 = 0.95802

Para o segundo:

a 2 = b 2 - b 1 3 h 2 = 0.02828

c 2 = f x 2 - f x 1 h 2 + h 2 2 b 2 + b 1 3 = 0.34456

d 2 = f x 2 = 1.09861

E por fim para o terceiro:

a 3 = b 3 - b 2 3 h 3 = - 0.09393

c 3 = f x 3 - f x 2 h 3 + h 3 2 b 3 + b 2 3 = 0.41501

d 3 = f x 3 = 1.29438

Passo 10

Juntando tudo numa função só:

S 3 x = s 1 x = 0.06565 x + 0.5 3 + 0.098476 x + 0.5 2 + 0.22488 x + 0.5 + 0.95802 ,       x ∈ - 1 , - 0.5 s 2 x = 0.02828 x 3 + 0.140897 x 2 + 0.34456 x + 1.09861 ,       x ∈ - 0.5,0 s 3 x = - 0.09393 x - 0.5 3 + 0.41501 x - 0.5 + 1.29438 ,       x ∈ 0,0.5

Resposta

a S 3 x = s 1 x = 1 + 3.43656 x ,   x ∈ 0,0.5

b S 3 x = s 1 x = 1.06641 - 1.0625 x ,   x ∈ - 0.25,0.25

c S 3 x = s 1 x = 4.38125 x - 0.2 3 + 1.3144 x - 0.2 2 - 2.6198 x - 0.2 - 0.5608 ,       x ∈ 0.1,0.2 s 2 x = - 4.38125 x - 0.3 3 - 2.4884 x - 0.3 - 0.814 ,       x ∈ 0.2,0.3

d S 3 x = s 1 x = 0.06565 x + 0.5 3 + 0.098476 x + 0.5 2 + 0.22488 x + 0.5 + 0.95802 ,       x ∈ - 1 , - 0.5 s 2 x = 0.02828 x 3 + 0.140897 x 2 + 0.34456 x + 1.09861 ,       x ∈ - 0.5,0 s 3 x = - 0.09393 x - 0.5 3 + 0.41501 x - 0.5 + 1.29438 ,       x ∈ 0,0.5

Exercícios de Livros Relacionados

A tabela a seguir foi obtida da observação de determinado fenômeno que se sabe é regido pela equação: E = a x + b y Sabendo que: i ) Determine pelo método dos mínimos quadrados aeb . i i ) Qual o erro
Considere a tabela:a) Determinar o polinômio de interpolação, na forma de Lagrange, sobre todos os pontos; b) Calcular f ( 3.5 ) .