Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Spline Cúbica Interpolante

Ver Teoria
Exercício 312

Enunciado

Encontrar uma aproximação para f 0.25 por spline cúbica natural na tabela:

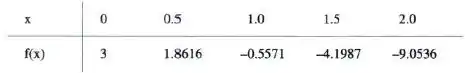
Passo 1

Primeiro definimos:

x 0 = 0 ; x 1 = 0.5 ; x 2 = 1.0 ; x 3 = 1.5 ; x 4 = 2.0

E como o espaçamento entre os pontos é o mesmo, temos h i = h = 0.5 . Substituindo no sistema A x = b :

A = 1 0 0 0 0 h 1 2 h 1 + h 2 h 2 0 0 0 h 2 2 h 2 + h 3 h 3 0 0 0 h 3 2 h 3 + h 4 h 4 0 0 0 0 1 = 1 0 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0 1

b = 3 0 f x 2 - f x 1 h 2 - f x 1 - f x 0 h 1 f x 3 - f x 2 h 3 - f x 2 - f x 1 h 3 f x 4 - f x 3 h 4 - f x 3 - f x 2 h 3 0 = 0 - 7.6818 - 7.3374 - 7.2798 0

Passo 2

Resolvemos então o sistema linear:

1 0 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0.5 2 0.5 0 0 0 0 1 b 0 b 1 b 2 b 3 b 4 = 0 - 7.6818 - 7.3374 - 7.2798 0

E obtemos que:

b 0 b 1 b 2 b 3 b 4 = 0 - 3.327 - 2.055 - 3.126 0

Passo 3

Agora repare que ele pede o valor em x = 0.25 que está entre x 0 e x 1 , logo precisamos do valor de s 1 0.25 .

Aplicando as fórmulas:

a 1 = b 1 - b 0 3 h 1 = - 2.218

c 1 = f x 1 - f x 0 h 1 + h 1 2 b 1 + b 0 3 = - 3.3858

d 1 = f x 1 = 1.8616

Passo 4

Juntando tudo temos:

s 1 x = - 2.218 x - 0.5 3 - 3.327 x - 0.5 2 - 3.3858 x - 0.5 + 1.8616

s 1 0.25 = 2.5348

Resposta

s 1 0.25 = 2.5348

Exercícios de Livros Relacionados

A tabela a seguir foi obtida da observação de determinado fenômeno que se sabe é regido pela equação: E = a x + b y Sabendo que: i ) Determine pelo método dos mínimos quadrados aeb . i i ) Qual o erro
Considere a tabela:a) Determinar o polinômio de interpolação, na forma de Lagrange, sobre todos os pontos; b) Calcular f ( 3.5 ) .