(Adaptado) Um componente eletrônico na forma de um disco com de diâmetro dissipa quanto montado sobre um grande bloco de uma liga de alumínio (2024), cuja temperatura é mantida a .
A configuração de montagem é tal que há uma resistência de contato de na interface entre o componente eletrônico e o bloco.
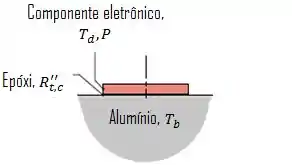
Calcule a temperatura que o componente atingirá, supondo que toda a potência gerada pelo componente deva ser transferida por condução para o bloco.
Passo 1
Como temos a taxa de transferência de calor, a temperatura do componente pode ser calculada utilizando a seguinte expressão:
Vamos calcular as resistências térmicas do circuito.
Passo 2
A resistência de contato será dada por:
Para a resistência bidimensional no disco, vamos usar o caso 10 da tabela, onde o fator de forma vale . Assim:
Passo 3
Finalmente, a temperatura do componente será:
![]()