Um furo de diâmetro é perfurado através do centro de um bloco sólido de seção transversal quadrada com de lado. O furo atravessa o comprimento do bloco, que é de .
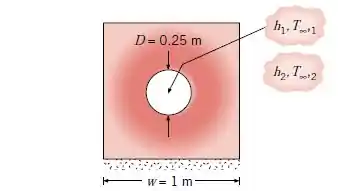
O bloco tem condutividade térmica . As superfícies externas estão expostas ao ar ambiente, com e , enquanto óleo quente escoa através do furo podendo ser caracterizado por e .
Determine a taxa de transferência de calor e as temperaturas superficiais correspondentes.
Passo 1
O calor é transferido do óleo para a superfície interna do bloco por convecção, da superfície interna para a externa por condução bidimensional, e da superfície externa do bloco para o ambiente por convecção. Assim, o circuito térmico pode ser representado por:
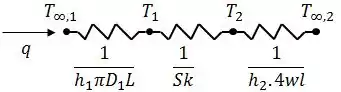
Assim, a taxa de transferência de calor pode ser dada por:
Onde é a resistência térmica total do circuito, sendo a soma das seguintes contribuições:
Para o fator de forma, de acordo com o caso 6 da tabela, temos que:
Dessa forma, a resistência térmica bidimensional será:
Logo, a taxa de transferência de calor será:
![]()
Passo 2
As temperaturas das superfícies podem ser definidas por:
![]()
![]()