Um iglu é construído na forma de um hemisfério, com raio interno de e paredes de neve compacta com uma espessura de .
No interior do iglu, o coeficiente de transferência de calor nas superfícies é de ; no lado de fora sob condições de ventos normais, ele é de . A condutividade térmica da neve compacta é de .
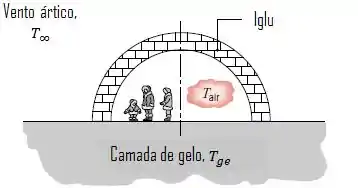
A temperatura da camada de gelo sobre a qual o iglu se encontra é de e a sua condutividade térmica é a mesma da neve compactada.
Considerando que os corpos ocupantes do iglu forneçam uma fonte contínua de calor de no interior do iglu, calcule a temperatura do ar no seu interior quando a temperatura do ar externo é de . Certifique-se de levar em consideração as perdas de calor pelo chão do iglu.
Passo 1
Do calor fornecido do sistema pelos ocupantes, parte flui para o exterior do iglu e parte flui para a camada de gelo. Assim, podemos representar o circuito térmico da seguinte forma:
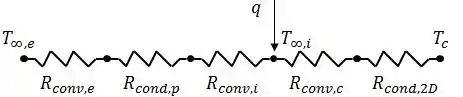
Dessa forma, podemos escrever a taxa de transferência de calor como:
Vamos calcular cada uma das resistências térmicas separadamente, beleza?
Passo 2
Considerando que estamos trabalhando com uma casca semiesférica, teremos:
Convecção externa:
Condução através da parede:
Convecção entre a parede interna do iglu e o ar interno:
Convecção entre o ar interno e o solo:
Condução bidimensional na camada de gelo:
De acordo com o caso 10 da tabela, . Dessa forma, a resistência térmica para esse caso será:
Passo 3
Substituindo todos os valores, teremos:
Agora é só arrumar a casa:
![]()