Um fluido quente escoa através de canais circulares em uma peça de ferro fundido com espessura , que apresenta um contato deficiente com as placas de cobertura , que têm espessura .

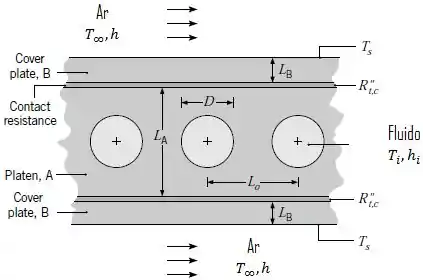
Os canais possuem diâmetro e o espaçamento entre as linhas de centro de canais adjacentes é . As condutividades térmicas dos materiais são e , enquanto a resistência de contato entre os dois materiais é de .

O fluido quente está a e o coeficiente de transferência de calor por convecção é de . O fator de forma entre um canal e a superfície superior, e a inferior, da peça é .

Determine a taxa de transferência de calor a partir de um único canal, por unidade de comprimento da peça na direção normal à página, .

Determine a temperatura da superfície externa da placa de cobertura, .

Determine a taxa de transferência de calor a partir de um único canal, por unidade de comprimento da peça na direção normal à página, .

Como o calor está sendo transferido tanto para a superfície superior, quanto para a inferior, podemos analisar o circuito considerando a transferência de calor entre a metade superior do duto e a superfície superior da placa.

Fazendo isso, teremos o seguinte circuito térmico:

Onde é a taxa de transferência de calor por unidade de comprimento. Estamos fazendo dessa forma porque o problema não nos forneceu a profundidade do sistema.

Além disso, o fator de forma dado pelo problema considera toda a superfície do duto. Nesse caso, como estamos considerando somente a metade superior do duto:

Dessa forma, a taxa de transferência de calor será:

Onde a resistência térmica total será a soma de todas as resistências térmicas, dadas por:

Repara que é o coeficiente de convecção do ar, que é tabelado.

Assim, a taxa de transferência de calor por unidade de comprimento será:

Repara que consideramos como , já que o problema não forneceu esse dado.