Água quente é transportada de uma estação de cogeração de potência para usuário comerciais e industriais através de tubos de aço com diâmetro . Cada tubo encontra-se no centro de um bloco de concreto de seção transversal quadrada .
As superfícies externas do concreto estão expostas ao ar ambiente, no qual e .
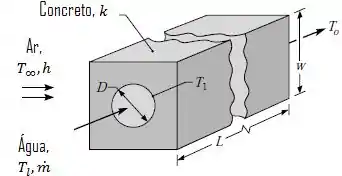
Sendo a temperatura de entrada da água escoando através do tubo igual a , qual é a perda de calor por unidade de comprimento do tubo na proximidade da entrada? A temperatura do tubo pode ser considerada para ser igual à da entrada da água.
Se diferença entre as temperaturas de entrada e de saída da água escoando através de um tubo com de comprimento não puder exceder os , estime a vazão mássica mínima permitida . Um valor de pode ser usado para o calor específico da água.
Passo 1
Sendo a temperatura de entrada da água escoando através do tubo igual a , qual é a perda de calor por unidade de comprimento do tubo na proximidade da entrada? A temperatura do tubo pode ser considerada para ser igual à da entrada da água.
A taxa de transferência de calor pode ser calculada da seguinte forma:
A resistência térmica de convecção vale:
Para a resistência de condução bidimensional, vamos considerar o caso 6 da tabela do fator de forma, onde o mesmo vale . Assim:
Assim, a taxa de transferência de calor será:
Como queremos a taxa de transferência de calor por unidade de comprimento . Dividindo os dois lados da equação por :
![]()
Passo 2
Se diferença entre as temperaturas de entrada e de saída da água escoando através de um tubo com de comprimento não puder exceder os , estime a vazão mássica mínima permitida . Um valor de pode ser usado para o calor específico da água.
Sabendo a diferença entre as temperaturas de entrada e saída, podemos calcular a vazão mássica da seguinte forma:
![]()
Resposta