Um homem deseja cercar seu terreno na forma de um triângulo retângulo com um muro. O maior lado do triângulo que mede metros está encostado em um riacho e, portanto, não precisa ser cercado. Quantos metros de muro deverão ser construídos sabendo que o menor lado mede metros?
Passo 1
Primeiramente, devemos aplicar o teorema de Pitágoras para descobrir o valor do lado restante.
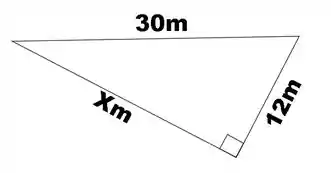
Passo 2
Agora precisamos encontrar o perímetro do triângulo:
O comprimento total do muro será o perímetro do triângulo menos o lado encostado no riacho:
Resposta
metros.