30. Sejam , e os lados de um triângulo retângulo, onde é a hipotenusa. Se o triângulo tem perímetro igual a , indique a área deste triângulo em função da hipotenusa.
Passo 1
Oi, galerinha! Tudo bom? O enunciado nos descreveu o seguinte triângulo retângulo:
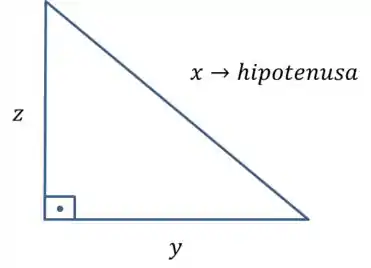
E nos disse que o perímetro é igual a , ou seja,
Agora precisamos encontrar a área deste triângulo. Lembrando que a área do triangulo é dada por:
Ou seja, pelos nosso triângulo, temos que
Bora lá!
Passo 2
Para começar, temos que nos atentar a um ponto, o enunciado pede para que a área deste triângulo em função da hipotenusa. Ou seja, vamos ter que encontrar uma relação dos outros lados com a hipotenusa .
Para isso, vamos usar o nosso famoso Teorema de Pitagoras, que nos diz que a soma do quadrado do catetos é igual ao quadrado a hipotenusa. Logo,
Isolando , ficamos com
Agora vamos isolar na fórmula do perimétrico
Igualando as duas equações, ficamos com
Abrindo o lado esquerdo,
Simplificando os termos comuns dos dois lados, ficamos com
Isolando do lado esquedor, ficamos com:
E
Então
Lembra que a área é dada por ? Então vamos isolar este termo,
Agora temos que deixar em função de , como o enunciado pede.
Passo 3
Galerinha, para deixar tudo em função de vamos lembrar de uma expressão que a gente já passou e está bem parecida com a expressão que achamos para área! Vamos olhar para expressão do perímetro:
Repara que passando e para o lado esquerdor e o para o direito, ficamos com
Substituindo essa expressão no cálculo da área ficamos com
Prontinho!