Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 37

Uma grande planta de potência estacionária com turbina a gás operando no ciclo Brayton fornece uma potência de 100   M W para um gerador elétrico. A temperatura mínima no ciclo é de 300   K , e a temperatura máxima é de 1600   K . A pressão mínima no ciclo é de 100   k P a e a razão de pressão no compressor é de 14 para 1 . Calcule a saída de potência da turbina. Que fração da saída de potência da turbina é requerida para acionar o compressor? Qual é o rendimento térmico do ciclo?

Passo 1

Fala, galera! Vamos resolver essa questão.

Galera, vamos começar analisando nosso ciclo:

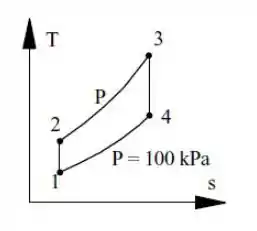
Aqui nós temos, nossa temperatura mínima:

T 1 = 300   K

E nossa temperatura máxima:

T 3 = 1600   K

Além disso, temos a razão entre as pressões:

P 2 P 1 = 14

Passo 2

Beleza, galera. Nós sabemos que o processo é isentrópico, ou seja,

s 1 = s 2

Dessa forma, podemos utilizar a relação das temperaturas:

T 2 = T 1 P 2 P 1 k - 1 k

Substituindo os valores:

T 2 = 300 ∙ 14 1,4 - 1 1,4 = 300 ∙ 14 0,286

T 2 = 638,1   K

Vamos utilizar a constante c p 0 = 1,004   k J / k g K para calcular o trabalho do compressor:

w c = h 2 - h 1 = c p 0 ( T 2 - T 1 )

w c = 1,004 ∙ ( 638,1 - 300 )

w c = 339,5   k J / k g

Passo 3

Vamos usar novamente a relação de entropia constante, para a expansão adiabática reversível na turbina:

s 3 = s 4

Logo,

T 4 = T 3 P 4 P 3 k - 1 k

Substituindo os valores:

T 4 = 1600 ∙ 1 14 0,286

T 4 = 752,2   K

E o trabalho na turbina será:

w T = h 3 - h 4 = c p 0 ( T 3 - T 4 )

w T = 1,004 ∙ ( 1600 - 752,2 )

w T = 851,2   k J / k g

Portanto, o trabalho líquido do ciclo será:

w l í q = w T - w c

w l í q = 851,2 - 3 39,5

w l í q = 511,7   k J / k g

Passo 4

Agora vamos considerar o fluxo máximo para calcular a potência na turbina e no compressor:

m ˙ = W ˙ l í q w l í q = 100000 511,7 = 195,4   k g / s

W ˙ T = m ˙ w T = 195,4 ∙ 851,2 = 166,32   M W

W ˙ c = m ˙ w c = 195,4 ∙ 339,5 = 66,3   M W

E a relação de potência entre turbina e compressor será:

w c w T = 339,5 851,2 = 0,399

A energia que entra é dada por:

q H = c p 0 T 3 - T 2

q H = 1,004 ∙ ( 1600 - 638,1 )

q H = 965,7   k J / k g

E seu rendimento:

η = w l í q q H = 511,7 965,7

η = 0 , 530

E concluímos o exercício! 😉

Resposta

W ˙ T = 166,32   M W

w c w T = 0,399

η = 0,530

Exercícios de Livros Relacionados

Ar entra a 310Ke100k P a no compressor de um motor de turbina a gás com regeneração, onde é comprimido até 900k P ae650K . O regenerador tem uma efetividade de 80 % , e o ar entra na turbina a 1.400K
Repita o P r o b . 9 – 118 para um regenerador com efetividade de 70 % .
Um motor de turbina a gás funciona segundo um ciclo Brayton ideal com regeneração, como mostrado na F i g .P 9 – 109 . O regenerador é então rearranjado para que as correntes de ar dos estados2e5 entr
Uma usina de potência com turbina a gás opera em um ciclo Brayton ideal com regeneração ( ϵ =100% ) usando ar como fluido de trabalho. O ar entra no compressor a 95k P ae290K , e na turbina, a 760k P
Uma usina de potência com turbina a gás operando em um ciclo Brayton simples tem uma razão de pressão igual a 7 . Em um certo momento, ar entra no compressor a0° Ce100k P a . A temperatura máxima do c