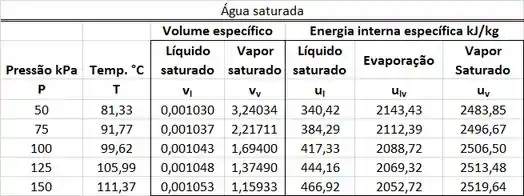
Água líquida saturada a entra em um tanque rígido com uma velocidade de através de uma tubulação com e a uma altura de em relação ao solo. A água sai do tanque como líquido saturado a mesma pressão da sua entrada por um tubo com de diâmetro e a uma altura de em relação ao solo. A área da seção transversal do tanque rígido vale . O nível da água do tanque desce a uma velocidade de . Determine a taxa de variação da energia da água do tanque rígido, considerando que a água do interior do tanque também permanece saturada a a todo momento e que todo o processo é adiabático.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de variação da energia da água do tanque rígido . A figura abaixo mostra todos os dados que temos para calcular esse valor.
é a velocidade da água entrando no tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão da água entrado no tanque rígido. A água sai do tanque rígido por um tubo de diâmetro igual a a uma altura do chão. é a pressão dessa água. é a área da seção transversal e é a velocidade com a qual o nível da água do tanque desce.
Ela é negativa, porque a altura desce. Logo, a altura varia negativamente.

Calcularemos através da primeira lei da termodinâmica aplicada ao volume de controle. No próximo passo, veremos essa equação.
Passo 2
A fórmula da taxa de variação da energia do tanque se encontra abaixo. Ela é a primeira lei da termodinâmica aplicada ao volume de controle.
onde é a taxa de energia que entra no tanque por causa de entrada de água, é a taxa de energia que sai no tanque por causa de saída de água e é a taxa de trabalho que a água do tanque realiza.
As fórmulas de e encontram-se abaixo.
é a vazão mássica, é o volume específico e é a energia interna específica da água que entra no tanque. é a vazão mássica, é o volume específico, é a energia interna específica e é a velocidade da água que sai do tanque. é a aceleração da gravidade da Terra.
No próximo passo vamos aprender como encontrar os valores de alguns termos das fórmulas!
Passo 3
Os valores de , , e estão presentes na tabela de saturação. está na mesma linha que a pressão de e na mesma coluna que o volume específico . é igual a , porque a água que entra e a água que sai estão no mesmo estado!

e estão na mesma linha que a pressão de e na mesma coluna que a energia interna específica .
Vamos aprender a calcular e no passo seguinte!
Passo 4
Na verdade, não precisa ser calculado! Como o enunciado diz que o processo de troca de massa com o ambiente é adiabático, vale zero.
é igual à massa específica da água multiplicada pela velocidade da água multiplicada pela área de passagem da água . Esse área pode ser calculada através do diâmetro do tubo pelo qual a água passa.
Além disso, as massas específicas são o inverso dos volumes específicos.
Passo 5
Como o tanque recebe e rejeita quantidades diferentes de água líquida, o volume de água do tanque varia a uma taxa igual a . Isso significa que a fronteira da água do tanque se mexe e a água realiza trabalho por movimento de fronteira a uma taxa igual a .

Como o enunciado diz que a água permanece sempre a mesma pressão de , esse trabalho é isobárico. Logo, a quantidade de energia por trabalho que o vapor recebe , quando a fronteira se movimenta pode ser calculado pela seguinte fórmula.
é a variação de volume da água do tanque. No entanto, nós não sabemos quando vale nem . Então como fazemos para transformar essa fórmula em uma equação que tenha o dado informado pelo enunciado () e a taxa de trabalho precisamos achar ?

O primeiro passo para transformar a fórmula antiga é dividir todos os termos dessa equação pelo intervalo de tempo de duração processo .
O passo final é fazer o intervalo de tempo ficar cada vez menor. No limite, quando tende a zero, essas divisões viram derivadas! Ou seja, elas viram as taxas de variação em relação ao tempo!
, e serão calculadas no próximo passo.
Passo 6
pode ser calculada através da equação de conservação de massa para volumes de controle.
No entanto, a massa específica da água do tanque é constante e vale a mesma coisa que a massa específica , porque as duas águas estão saturadas a . Por isso:
No entanto o volume é igual à área da seção transversal do tanque vezes a altura da água presente nele . Por causa disso, achamos uma fórmula para .
A vazão mássica da água que sai do tanque também pode ser calculada por uma fórmula muito parecida com a fórmula de . Com essa equação, conseguimos criar uma fórmula para .
Agora que aprendemos tudo isso, podemos começar a fazer as contas!
Passo 7
A primeira parte dos cálculos é de encontrar , , e na tabela de saturação.
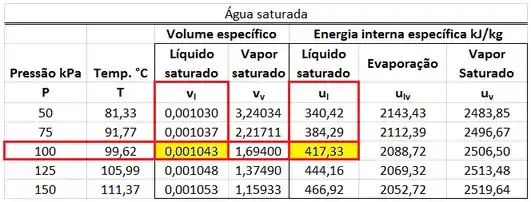
No próximo passo, vamos calcular as vazões.
Passo 8
Começamos os cálculos das vazões pelo cálculo das massas específicas.
Com esses valores, podemos achas as vazões mássicas.
Sabendo essa vazão, podemos calcular e .
Agora podemos encontrar e .
Passo 9
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
Cuidado! Para as parcelas de energia potencial e energia cinética ficarem na unidade certa na fómula de , precisamos dividir cada uma dessas parcelas por mil!
Vamos partir para o cálculo de e da taxa de variação de energia do tanque !
Passo 10
pode ser achado a partir da fórmula:
No entanto pode ser calculado pela fórmula:
Logo:
Substituindo os dados que conhecemos, encontramos:
Por fim, vale: