Água líquida saturada a entra em um tanque rígido com uma velocidade de através de uma tubulação com de diâmetro. A água é aquecida dentro do tanque e sai dele como vapor saturado a com uma velocidade de por um tubo com de diâmetro. Considerando a energia potencial da água desprezível, calcule a taxa de variação da energia do tanque rígido devido à entrada e à saída de água.
Passo 1
O enunciado pede que a gente calcule o valor da taxa de variação da energia do tanque rígido devido à entrada e à saída de água . Perceba que o tanque também recebe energia por calor, porque é aquecido. No entanto, o enunciado só quer saber da parcela de energia que o tanque troca através da entrada e da saída de água. A figura abaixo mostra todos os dados que temos para calcular esse valor.
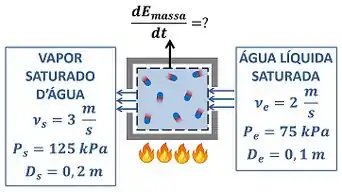
é a velocidade da água líquida saturada entrando no tanque rígido por um tubo de diâmetro igual a . é a pressão da água entrado no tanque rígido. é a velocidade do vapor saturado d’água saindo do tanque rígido por um tubo de diâmetro igual a . é a pressão desse vapor.
No próximo passo, veremos qual fórmula é usada para calcular .
Passo 2
A fórmula da taxa de variação da energia do tanque devido à entrada e saída de massa se encontra abaixo.
onde é a taxa de energia que entra no tanque por causa de entrada de água e é a taxa de energia que sai no tanque por causa de saída de água.
As fórmulas de e encontram-se abaixo. A energia potencial da água não está presente nessas fórmulas, porque o enunciado falou que ela é desprezível.
é a vazão mássica, é o volume específico e é a energia interna específica da água líquida que entra no tanque. é a vazão mássica, é o volume específico e é a energia interna específica do vapor d’água que sai do tanque.
No próximo passo vamos aprender como encontrar os valores de alguns termos das fórmulas!
Passo 3
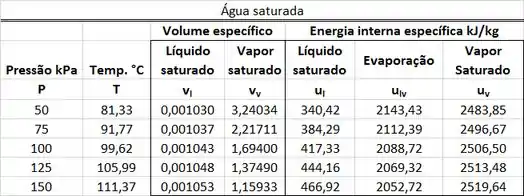
Os valores de , , e estão presentes na tabela de saturação. está na mesma linha que a pressão de e na mesma coluna que o volume específico . está na mesma linha que a pressão de e na mesma coluna que o volume específico . está na mesma linha que a pressão de e na mesma coluna que a energia interna específica . está na mesma linha que a pressão de e na mesma coluna que a energia interna específica .

Vamos aprender a calcular e no passo seguinte!
Passo 4
e são calculadas por fórmulas muito parecidas! Os dois são igual à massa específica da água multiplicada pela velocidade da água multiplicada pela área de passagem da água . Esse área pode ser calculada através do diâmetro do tubo pelo qual a água passa.
Além disso, as massas específicas são o inverso dos volumes específicos.
Agora que aprendemos tudo isso, podemos começar a fazer as contas!
Passo 5
A primeira parte dos cálculos é de encontrar , , e na tabela de saturação. e são obtidos abaixo.
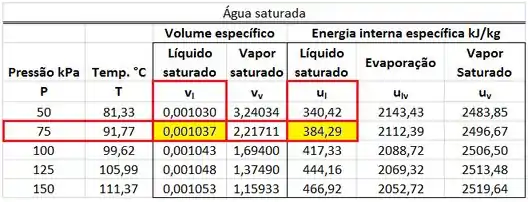
e são obtidos abaixo.
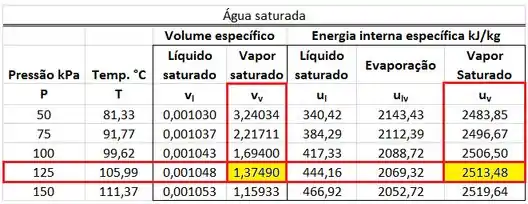
No próximo passo, vamos calcular as vazões e a taxa de variação de energia do tanque .
Passo 6
Começamos os cálculos das vazões pelo cálculo das massas específicas.
Com esses valores, podemos achas as vazões mássicas.
Agora podemos encontrar e .
Cuidado! Para a parcela de energia cinética ficar na unidade certa na fómula de e , precisamos dividir a parcela por mil!
Por fim, vale: