Encontre a função de transferência e a resposta ao degrau unitário do sistema cuja equação das diferenças é dada por
Onde e são a saída e a entrada do sistema, respectivamente.
Passo 1
Uma função de transferência é a razão entre a saída e a entrada de um sistema. No tempo discreto, ela é obtida aplicando a transformada Z em uma equação das diferenças, considerando as condições iniciais nulas, e dividindo a saída pela entrada. Logo, será:
Onde é a tranformada Z de e , de .
Para resolver o exercício, primeiramente aplicaremos a função do MATLAB na equação de diferenças para encontrarmos a transformada de e , que indicaremos por e , respectivamente. Em seguida, manipularemos a equação para obtermos , que será a função de transferência .
Para obter a resposta ao degrau unitário do sistema, calcula-se produto entre e a transformada Z do degrau do unitário. Em seguida, usamos a função para calcular sua transformada inversa, que será a solução do exercício.
Passo 2
Vamos rearranjar a equação, jogando todos os termos para a esquerda:
No MATLAB, vamos aplicar a função em cada termo da equação individualmente, pois dessa forma conseguiremos fazer a manipulação algébrica. Lembrando que tem a sintaxe:
Ela retorna a transformada Z da função , armazenando-a na variável . Quando não tem mais nenhuma entrada em além de , o MATLAB assume que a variável independente de é e fará que a transformada Z seja em função de .
A transformada Z dos termos da equação das diferenças será identificada assim:
Onde indica a transformada Z. Logo:
Considerando tudo isso, em um novo script, digite as linhas de código:

Na primeira linha, definimos as variáveis simbólicas , e (indicamos que e são em função de ).
Na segunda linha, assumimos que , para que o degrau unitário , que será usado mais pra frente, seja igual a .
Na terceira, quarta e quinta linha, a transformada Z de cada um dos termos da equação das diferenças rearranjada é calculada, sendo armazenada em , e .
Na sexta linha, montamos a transformada Z da equação das diferenças usando , e , fazendo-a igual a . A transformada da equação é armazenada na variável .
Vamos ver como ficou a equação após a aplicação da transformada Z? Execute o programa e imprima no Command Window:

Passo 3
Podemos simplificar : note que tem termos que tem exatamente a mesma estrutura da função e que representam transformadas que podem ser substituídas por uma única letra, indicando que é a transformada de uma função de . representa a transformada Z de , podendo ser substituído por . No caso, chamaremos só de .
Já representa a transformada Z de , podendo ser substituído por . Como fizemos para , chamaremos só de .
Adicione os comandos abaixo em seu programa para fazer a substituição:
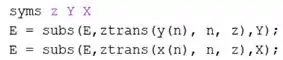
Primeiramente, criamos mais três variáveis simbolicas: , e . Em seguida, usamos a função para pedir ao MATLAB que substitua em a expressão por . Logo abaixo, fazemos a mesma coisa para . O resultado da substituição é armazenado em , ficando no lugar da expressão antiga.
E tem mais coisa que podemos substituir em . Precisamos encontrar a função de transferência do sistema, que é determinada considerando as condições iniciais nulas. Logo, . Para fazer a substiuição, adicione ao seu programa a linha de código:
![]()
Com este comando, substituímos por em e armazenamos a nova expressão em , atualizando a equação. Executando o programa, podemos ver como está agora:

Bem mais bonitinho =)
Passo 4
Para calcular , precisamos dividir por . Em , a variável representa e podemos usar a função do MATLAB para isolá-la na equação. Adicione em seu código:
![]()
Com este comando, a função resolve a equação para a variável e armazena a solução em , atualizando seu valor. Na prática, isolamos na equação com este comando e passa a representar a expressão algébrica de . Rodando o programa, temos que é igual a:

Para definir , basta dividir por :
![]()
E temos que a função de transferência é igual a:
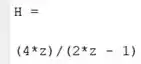
Passo 5
Com , podemos calcular a resposta ao degrau unitário do sistema, que é dada pelo produto entre e a transformada Z do degrau do unitário. Para criar o degrau unitário, usaremos a função , que tem a estrutura:
Ela cria um degrau unitário e o armazena em : quando , . Se , . Finalmente, para , . Como dissemos que , temos .
Após criar o degrau com , aplicamos nele para obter sua transformada Z.
Digite em seu programa os comandos:
![]()
Na primeira linha, criamos o degrau unitário e o armazenamos em . Em seguida, calculamos sua transformada Z e a registramos em .
Para encontrar a resposta ao degrau, inclua no seu programa o comando:
![]()
é o produto entre e e representa a transformada Z da resposta ao degrau unitário.
Passo 6
Para finalizar, vamos calcular a transformada inversa de para encontrar , a resposta do sistema ao degrau unitário no domínio de tempo discreto.
Para encontrarmos , vamos usar a função do MATLAB em . A função tem a estrutura:
Ela retorna a inversa da transformada Z de , armazenando-a na variável . Quando não tem mais nenhuma entrada em além de , o MATLAB assume que a variável independente de é e fará que a inversa da transformada Z seja em função de .
Para encontrar , entre o comando:
![]()
Com este comando, o MATLAB calcula a inversa da transformada Z de e armazena o resultado em . Rodando o programa, é igual a:

Resposta
A função de transferência é igual a:
A resposta ao degrau unitário do sistema é: