Calcule a temperatura média de uma placa limitada pelos eixos cartesianos e pelas retas , sabendo que a temperatura em cada ponto obedece a função
Passo 1
Vamos organizar as informações que o problema deu pra gente e entender o que precisamos fazer. O enunciado pediu pra calcular uma temperatura média, certo? Então já imaginamos que vamos ter que usar a fórmula do valor médio:
No caso a nossa função vai ser a da temperatura dada:
Precisamos então determinar os limites da nossa região para poder calcular a integral dupla de e, por fim, calcular a área de , vamos lá?
Passo 2
Vamos descrever a nossa região , graficamente ela é assim:
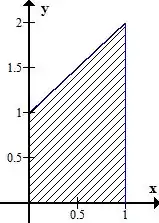
A maneira mais fácil de escolher os limites de integração vai ser pelo tipo , nesse caso, definimos como o intervalo entre zero e a função
Passo 3
Beleza, definidos os limites, podemos pensar na nossa integral dupla, lembrando que a função que o enunciado deu foi
Integrando em , vamos considerar como constante, com isso:
Para fazer essa integral aí, vamos ter que aplicar uma mudança de variável, fica assim:
Substituindo tudo isso, temos que:
Passo 4
Calculada a nossa integral dupla, vamos continuar o passo a passo calculando a área da região . Nessa questão aqui tem dois jeitos de fazer, vou mostrar os dois e você escolhe qual achou mais simples, beleza?
O primeiro é o que vai dar certo sempre! Aquele que, mesmo que o enunciado te dê a região mais bizarra do mundo a gente consegue calcular a área: pela integral dupla!
O segundo jeito é mais visual, percebe que a nossa região pode ser dividida em um quadrado e um triângulo assim:
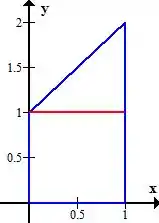
O quadrado tem lado igual a , portanto sua área é simples de calcular.
O triângulo tem base e altura iguais a também, portanto, podemos calcular a área da região como a soma das duas áreas!
Passo 5
Temos então o valor da integral e da área da região, agora é só jogar esses valores na fórmula do valor médio!