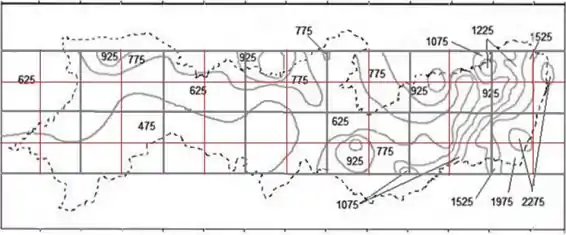
O mapa abaixo mostra a precipitação pluviométrica média anula em , para Pernambuco, em 2012. O Estado é aproximadamente um retângulo de . Usando a área retangular e as sub-divisões indicadas na figura, estime o valor médio da precipitação pluviométrica para o Estado como um todo, naquele ano. Use a aproximação do ponto médio.
Passo 1
A questão é bem específica no que ela quer que a gente faça, não é? Precisamos usar a aproximação do valor médio pra estimar... pasmem... o valor médio da precipitação no mapa.
Se não ficou muito claro o que a questão quer que a gente faça, vê se isso aqui ajuda:
Ao invés de medir a área de cada uma dessas regiões que o mapa mostra, que seria absurdamente difícil e só com um computador, o mapa foi dividido em quadrados e vamos considerar cada um deles como se tivesse um único índice pluviométrico!
“Ok, mas como vamos escolher qual índice colocar em cada quadrado?”
Vamos pegar exatamente o índice no ponto médio do quadrado! Olha só no caso desse primeiro aqui:
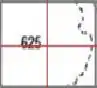
As linhas vermelhas só servem pra mostrar onde está o ponto médio, beleza?
Dá pra ver que elas se cruzam na região de , né? Então vamos considerar esse quadrado todo com índice de !
Pra organizar melhor vamos guardar os resultados por linhas e colunas , , portanto esse primeiro índice é o , pois está na linha e coluna .
Vamos repetir esse procedimento pra todas elas, vem comigo!
Passo 2
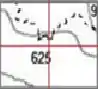
Olhando para o quadrado do lado, estamos agora na linha e coluna , portanto

Se olhar no mapa inteiro, esse ponto está na região


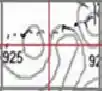
Essa imagem aí bate certinho na fronteira de e . Não tem problema, vamos considerar o índice total como a média entre esses dois valores
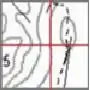
Também se encontra na fronteira aqui, vamos fazer a média de novo
Passo 3
Vamos agora para a linha de baixo





Fronteira de novo, fazendo a média

Mais uma fronteira aqui
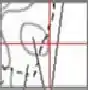
Pra acabar aqui
Passo 4
Juntando tudo no nosso novo mapa, olha só como fica

Simplificamos aquele mapa bizarro em 14 regiões com a mesma área, bem mais fácil de visualizar assim, não é?
O que a questão pede é a estimativa do valor médio da função. Pra fazer isso é só somar tudo e dividir pela quantidade de quadrados que temos, no caso .
Somando todos os termos da primeira linha
Agora para a segunda linha
Somando tudo e dividindo por 14