Observe o gráfico abaixo, que traça a concentração de determinada substância em função do tempo em um reator.
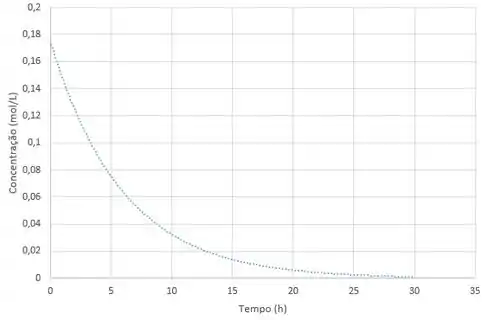
Com base no gráfico, responda:
a) A substância em questão é um reagente ou produto da reação que se procede no reator?
b) Qual a velocidade média, em relação a essa substância, nas 30 primeiras horas?
c) Determine a velocidade instantânea no tempo .
d) Determine a velocidade instantânea no tempo .
e) Considerando que o a curva de concentração x tempo obedeça a função , calcule a velocidade instantânea no tempo igual a 10 h.
Passo 1
a) Pelo gráfico a gente pode ver que a concentração da substância diminui com o passar do tempo. Portanto, a substância está sendo consumida (e não produzida) no meio.
A substância é um reagente.
Passo 2
b) Para a substância em questão, temos:
Portanto, a velocidade média em relação a essa substância pode ser calculada por:
Não esquece do menos, porque estamos falando de um reagente!
Passo 3
c) A velocidade instantânea é dada pela tangente da curva, no instante determinado.
Por exemplo, no instante , podemos traçar a tangente à curva, assim:
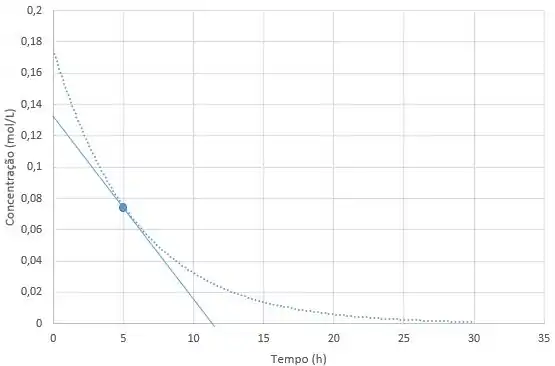
Claro que esse é um método aproximado. Mas dessa forma, podemos calcular a velocidade instantânea, que será dada pelo coeficiente angular da reta que a gente acabou de traçar.
Tal que a velocidade de consumo desse reagente no instante é .
Observe que uma velocidade de consumo negativa seria o mesmo que estar produzindo o cara, por isso usamos a velocidade positiva!
Passo 4
d) Para o tempo , mesmo procedimento!
Começamos traçando a curva tangente no ponto.
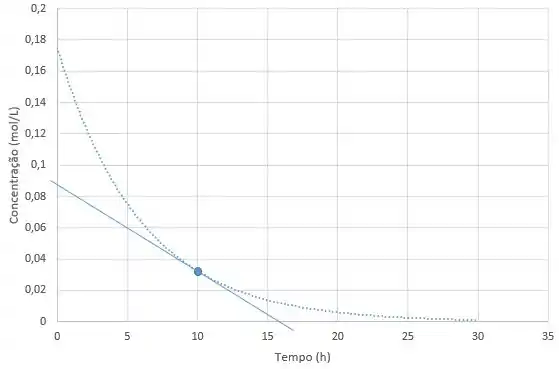
Tal que a velocidade de consumo desse reagente no instante é .
Passo 5
e) Se a gente conhece exatamente a função que representa a relação entre a concentração e o tempo, podemos calcular a velocidade instantânea pela derivada dessa função!!
Então, bora derivar:
E o valor da derivada para :
Tal que a velocidade de consumo desse reagente no instante é .
A diferença do valor calculado nos itens d e e deve-se às aproximações feitas no item d.
Resposta
a) Reagente
b)
c)
d)
e)