Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Função De Várias Variáveis

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos trocar uma ideia sobre funções de várias variáveis. Esse texto aqui vai ser bem introdutório, tá? Então fica confortável aí e vamos nessa!

⭐ Veja também ⭐

O que é uma função de várias variáveis?

Uma função de várias variáveis é aquela que relaciona múltiplas variáveis com um resultado.

Não ficou claro? Deixa eu explicar melhor.

Olha só, quando estudamos funções de uma variável só, do tipo:

Vemos que ela relaciona um número , que você fornece como entrada, a um outro número , que a função te fornece de volta na saída. Certo?

Similarmente, uma função de duas variáveis relaciona dois números , e , a um outro número . Como é o caso dessa funçãozinha aqui:

E isso você pode extrapolar pra quantas variáveis você quiser!

Então, de uma maneira geral, a função de várias variáveis é aquela que requer a entrada de vários números para retornar um outro número relacionado pela regra da função.

Como calcular funções de várias variáveis?

Pra resolver uma função de várias variáveis, basta substituir os valores iniciais nas respectivas variáveis.

Se tivermos uma função e quisermos calcular o valor de em , por exemplo, vamos substituir cada um desses valores na variável correspondente.

Mais pra frente, a gente vai aprender como saber se uma função de várias variáveis é contínua e se ela é diferenciável!

Pra ficar mais claro, se liga no exemplo 👇

Calcule o valor da função de três variáveis no ponto .

No ponto , a gente tem , e . Então é só substituir isso aí na nossa função!

Sem segredos, né?

Se quiser praticar um pouquinho mais, se liga nesse vídeo aqui com mais resoluções bem detalhadas 👇

Interpretação Gráfica

Como a gente viu até aqui, as funções de várias variáveis associam pontos em um espaço com pontos em outro espaço. O problema é que, quando trabalhamos com funções com mais que três variáveis, o negócio começa a ficar bem complicado de visualizar.

Acompanha o raciocínio aqui:

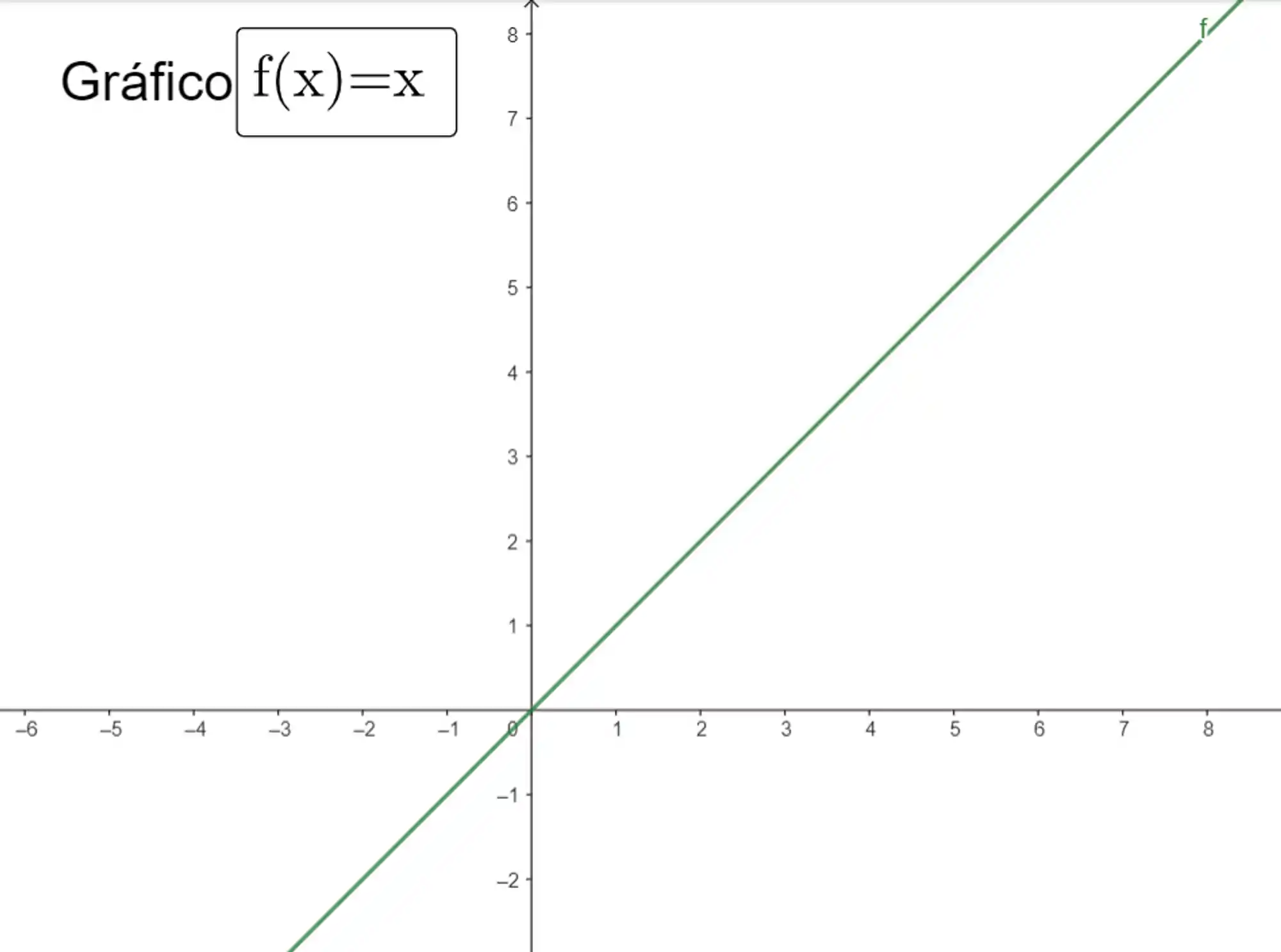
  • Função de uma variável 👉 o gráfico associa um número com um outro número. Para representarmos essas associações, precisamos de um gráfico com coordenadas cartesianas em duas dimensões .

Gráfico de uma função de uma variável.
Gráfico de uma função de uma variável.

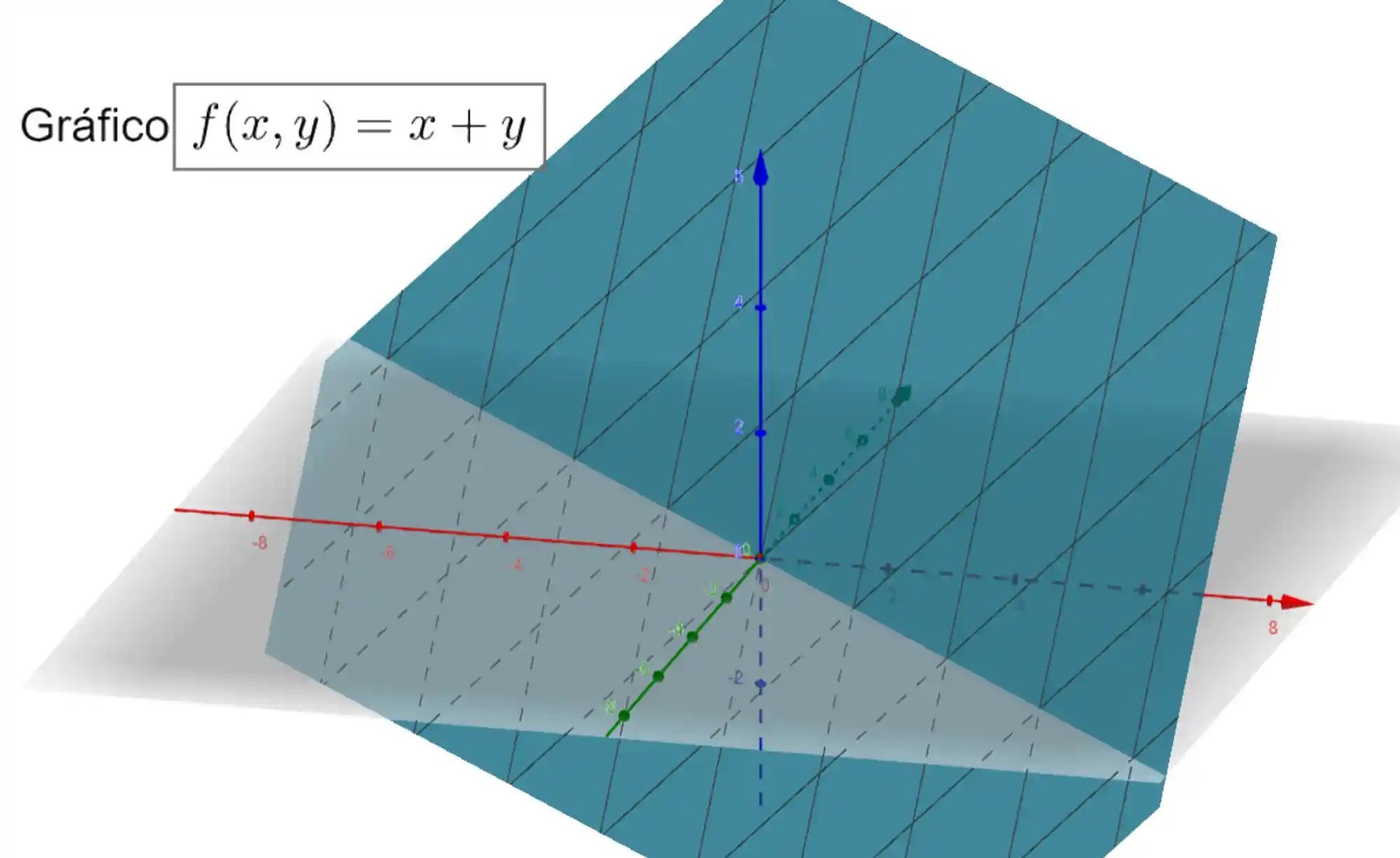
  • Função de duas variáveis 👉 o gráfico associa dois números com um outro número. Para representarmos essas associações, precisamos de um gráfico com coordenadas cartesianas em três dimensões

Gráfico de uma função de duas variáveis.
Gráfico de uma função de duas variáveis.

  • Função de três variáveis 👉 o gráfico associa três números com um outro número. Para representarmos essas associações, precisamos de um gráfico com coordenadas cartesianas em quatro dimensões .

Aí eu te pergunto, como é que a gente vai imaginar quatro dimensões e projetar isso em uma tela ou papel de duas dimensões???

O negócio já começa a ficar meio impossível pra nós seres humaninhos limitados, né?

Pode ficar tranquilo! Ninguém vai te pedir pra desenhar gráficos desses tipos não 😆

Interpretação Gráfica

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Considere a função

f x , y , z = x 2 y + 3 z y - x + 3

Calcule os valores de f nos pontos:

a) 0 ,   1 ,   0

b) - 1 ,   2 ,   4

c) 3 ,   - 3 ,   3

Passo 1

Pra cada ponto basta substituir os valores dados de x , y e z na função.

a)

f 0 ,   1 ,   0 = 0 2 . 1 + 3.0 . 1 - 0 + 3

⇒ f 0 ,   1 ,   0 = 0 + 0 - 0 + 3

⇒ f 0 ,   1 ,   0 = 3

Tranquilo? Vamos continuar!

Passo 2

b)

f - 1 ,   2 ,   4 = - 1 2 . 2 + 3.4 . 2 - - 1 + 3

⇒ f - 1 ,   2 ,   4 = 2 + 24 + 1 + 3

⇒ f - 1 ,   2 ,   4 = 30

Beleza, agora vamos pra letra c).

Passo 3

f 3 ,   - 3 ,   3 = 3 2 . - 3 + 3.3 . - 3 - 3 + 3

⇒ f 3 ,   - 3 ,   3 = - 27 - 27

⇒ f 3 ,   - 3 ,   3 = - 54

Sem mistério né?

Resposta

a) 3

b) 30

c) - 54

Exercício Resolvido #2

Hamilton Luiz Guidorizzi, Um Curso de Cálculo – Volume 2, 5ª ed. Rio de Janeiro: LTC – Livros Técnicos e Científicos Editora S.A., 2001, p. 152 - 1

Seja f x , y = 3 x + 2 y . Calcule

a) f 1 , - 1

b) f a ,   x

c) f x + h ,   y - f x , y h

d) f x ,   y + k - f x , y k

Passo 1

Basta substituir os valores na função!

a)

f 1 , - 1 = 3.1 + 2 . - 1

→ f 1 , - 1 = 3 - 2

→ f 1 , - 1 = 1

Passo 2

b)

Agora temos que calcular f x ,   y no ponto a ,   x . É como se o a fizesse o papel de x e o x fizesse o papel de y . Não muda nada, só basta ter cuidado pra não confundir os “ x ”:

f a ,   x = 3 a + 2 x

Passo 3

c)

Que tal a gente começar calculando f x + h ,   y ?

f x + h ,   y = 3 x + h + 2 y

→ f x + h ,   y = 3 x + 3 h + 2 y

Passo 4

Então vamos ter

f x + h ,   y - f x , y h = 3 x + 3 h + 2 y - 3 x + 2 y h

Ajeitando um pouco, isso dá:

3 x - 3 x + 2 y - 2 y + 3 h h = 3 h h

→ f x + h ,   y - f x , y h = 3

Passo 5

Essa daqui vai ser bem parecida. Temos

f x ,   y + k = 3 x + 2 y + k

→ f x ,   y + k = 3 x + 2 y + 2 k

Passo 6

Então nossa conta vai ser:

f x ,   y + k - f x , y k = 3 x + 2 y + 2 k - 3 x - 2 y k

⇒ f x ,   y + k - f x , y k = 2 k k = 2

Resposta

a) 1

b) 3 a + 2 x

c) 3

d) 2

Exercícios de Livros Relacionados

Fazer um esboço de algumas superfícies de nível da função w = x 2 + y 2 + z 2 . O que ocorre com os valores da função ao longo de semi-retas que partem da origem?
Identificar as afirmações verdadeiras:g) Todo ponto de acumulação de um conjunto A pertence a esse conjunto.
10- Considerando a função z = f x ,y = 7 - x 2 + y 2 ,0 ≤ x 2 + y 2 ≤ 16 , 25 - x 2 - y 2 ,16 ≤ x 2 + y 2 ≤ 25 b)Identifique a curva de nível que contém o pontoP 0 = ( 1 ,3 ) .
Encontrar uma função de várias variáveis que nos dê:e) O volume de um paralelepípedo retângulo de dimensão x , y e z .
Encontrar uma função de várias variáveis que nos dê:o comprimento de uma escada apoiada como na figura 1.35.