Fazer um esboço de algumas superfícies de nível da função . O que ocorre com os valores da função ao longo de semi-retas que partem da origem?

Para encontrarmos as superfícies de nível, precisamos igualar a função a e variar seu valor. Assim, variando de a , por exemplo, temos as seguintes curvas de nível:

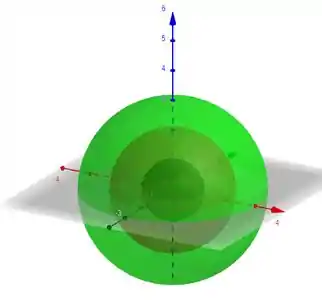
Ao longo das semi-retas que partem da origem, podemos observar, até mesmo pelo desenho acima, que os valores da função crescem à medida que nos afastamos da origem!