Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 1.4 - Ex. 1a
Encontrar uma função de várias variáveis que nos dê:
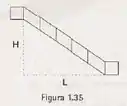
- o comprimento de uma escada apoiada como na figura 1.35.
Passo 1
Fala aí! Esse enunciado pediu pra gente observar a figura e encontrar uma função que nos dê o comprimento… Hummm… Olha só, essa escada tem uma altura H e um lado L, né?
A gente pode desenhar ela assim:
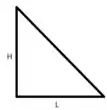
Show! Encontramos um triângulo retângulo! Aí a gente precisa lembrar do famoso Teorema de Pitágoras… Lembra dele? Ele diz que é a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa, matematicamente é isso aqui:
Passo 2
Mas quem é a hipotenusa? E os catetos?
Bom, a hipotenusa é o lado que fica de frente para o ângulo de , beleza? Olha ele aqui:
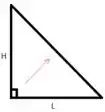
E os catetos são exatamente os dois lados que nós temos, olha:
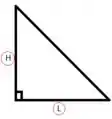
Show de bola! Então a hipotenusa é exatamente quem nós queremos achar, e usando o Teorema de Pitágoras podemos escrever ela como uma função dos catetos, né?
Passo 3
Vamos então reproduzir o teorema com os dados do nosso enunciado, chamando a hipotenusa de , que é o nosso comprimento, beleza?
Arrasamos! Então o comprimento é uma função do e do , ficando assim:
Prontinho!