Teoria
Uma elipse é uma figura geométrica que parece uma circunferência achatada! Ela tem essa carinha aqui:
Equação da Elipse
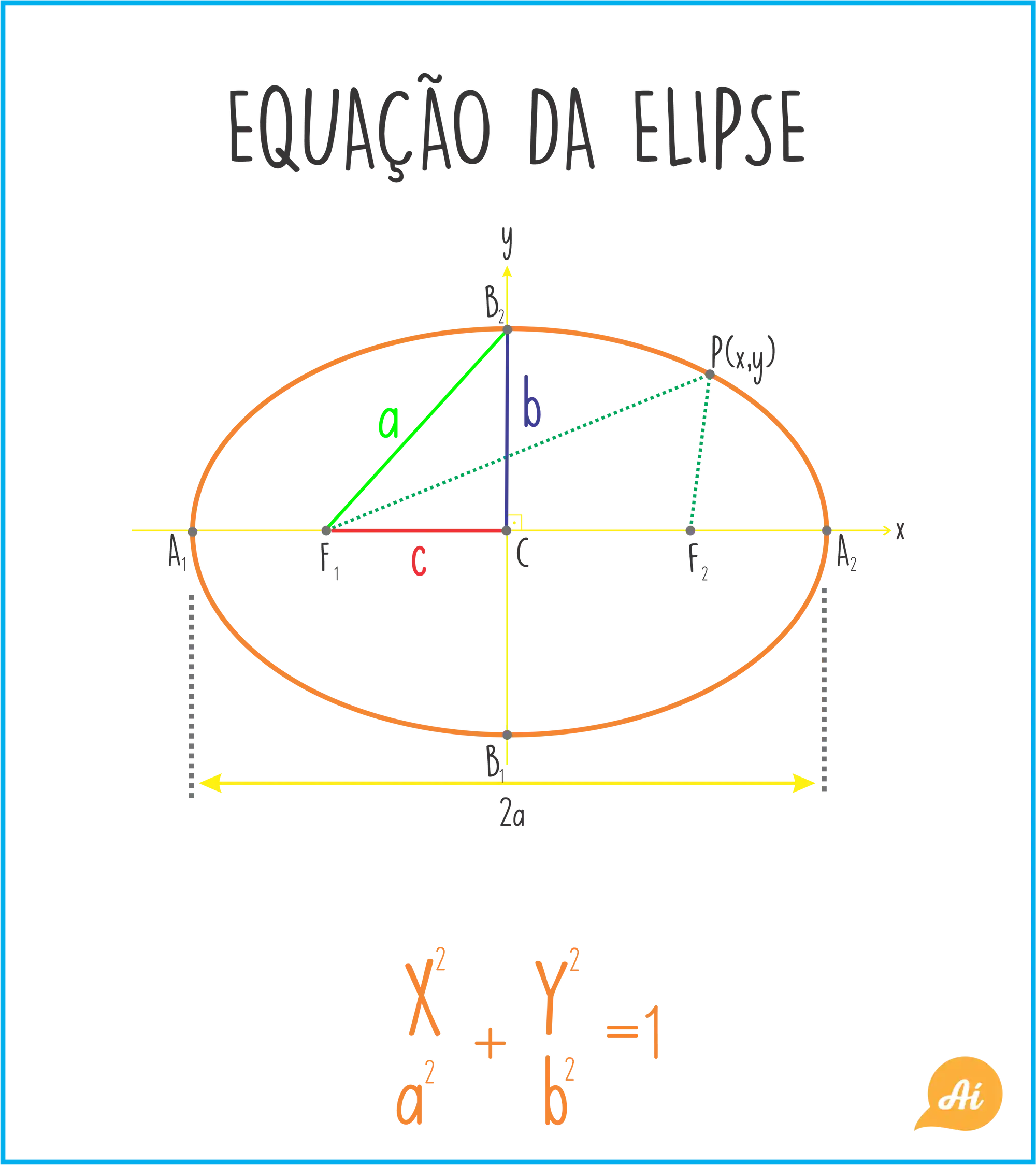
Na figura acima a gente pode ver a elipse e sua equação! Já deu pra perceber que “circunferência achatada” não é a definição mais completa! 🤣 🤣 🤣
-Mas, afinal o que significa todos esses pontos? Quem é esse “a” e “b” na equação da elipse? Como eu uso essa equação?
- Os pontos
e são chamados de focos; - A distância
entre os focos é chamada de distância focal; - O ponto
é o centro, ponto médio entre os focos; - Eixo maior é o segmento entre
e que tem comprimento ; - Eixo menor é o segmento entre
e que tem comprimento ; - Vértices são os pontos:
e
Temos também o que chamamos de excentricidade que é dada por:
Sendo $c
Agora vamos ver o que faz uma elipse ser uma elipse, ou seja, sua definição formal:
Considerando dois pontos distintos
Eu sei que ainda não ficou suuuper claro! Mas essa definição é bem importante e com exercícios e prática tudo fica mais fácil! O Responde Aí preparou um vídeo irado pra você aprender TUDO sobre Elipses de uma vez por todas, com exemplos, exercícios e muito mais! Dá só uma conferida! 👇
📢 Clique para ver mais:
Equação da Elipse
Lá em cima a gente mostrou uma elipse com o centro em
- Caso 1: O eixo maior está sobre o eixo dos
; - Caso 2: O eixo maior está sobre o eixo dos
; - Caso 3: Translação
Mas para qualquer caso, em toda a elipse vale a relação de Pitágoras:
Caso 1: O eixo maior está sobre o eixo
Para este caso vamos considerar a figura a seguir:
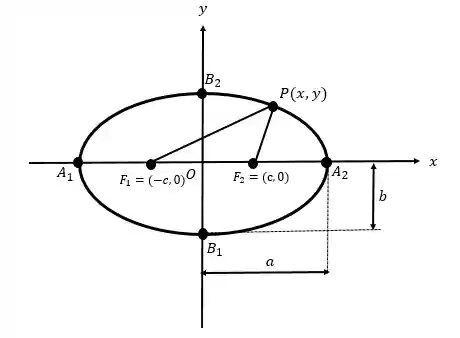
Seja
Substituindo o ponto
Que é a equação reduzida da elipse de centro na origem e eixo maior sobre o eixo
Caso 2: O eixo maior está sobre o eixo
Agora, se o eixo maior está sobre o eixo
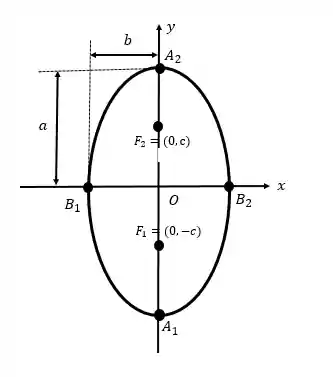
Utilizando novamente a definição de elipse, chega-se que a equação reduzida da elipse da figura é:
Novamente, vemos que nossos vértices continuam os mesmos do item anterior:
Note alguns detalhes importantes:
- O valor de
; é sempre o eixo maior; - Sempre o maior denominador da equação reduzida da elipse representa o
. Logo, se o maior valor está dividindo o isso significa que estamos no CASO 1, já se o maior denominador está dividindo o , então estamos no CASO 2.
Caso 3: Translação
Para terminar, vamos falar sobre a translação! Nesse caso temos duas possibilidades mostradas na figura a seguir:
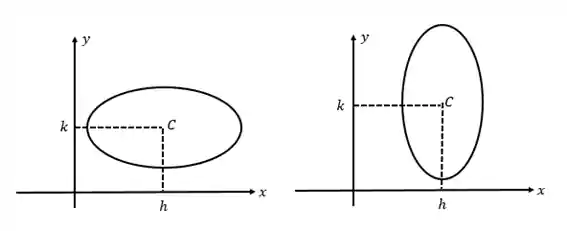
Uma translação nada mais é que deslocarmos o centro da elipse, ou seja, nos casos
Nossas equações ficarão:
Ou:
Agora vamos praticar com exercícios!?
Equação da Elipse
Exercícios Resolvidos
Exercício Resolvido #1
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 269-2.
Para as elipses dadas, determine os vértices, os focos, a excentricidade . Faça um esboço.
Passo 1
Bora começar a aquecer nossos neurônios sobre elipses!! Hehe
Temos quatro itens cada um com uma expressão de uma elipse e em cada item devemos determinar: vértices, focos, excentricidade e fazer um esboço.
Vamos comerçar!!

Passo 2
a)
Para começarmos esse exercício precisamos colocar a expressão na forma reduzida, ou seja, desse jeito:
Porque assim conseguiremos determinar os valores de e que precisamos para achar os elementos que queremos.
Então, vamos começar!!
Dividindo tudo por , temos:
Como deve ser sempre maior que , então:
Como deve ser maior que e está embaixo do então significa que estamos no caso 1, e teremos uma elipse com o seguinte formato:
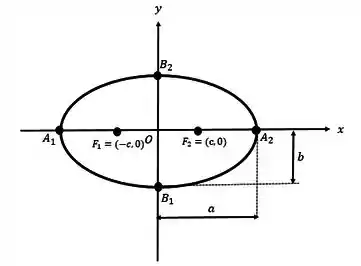
Pela figura, conseguimos determinar os focos e vértices
Temos o valor de e , mas para determinar os focos precisamos de . Mas, como vamos achar ?
Para achar vamos usar a seguinte relação das elipses: . Subsituindo os valores de e , temos:
Repare que o resultado seria , porém como e são distânciasnão faz sentido o valor negativo.
Agora sim, temos tudo o que precisamos é só substituir os valores e encontrar os focos, vértices e excentricidade.
E fazendo um esboço, temos:
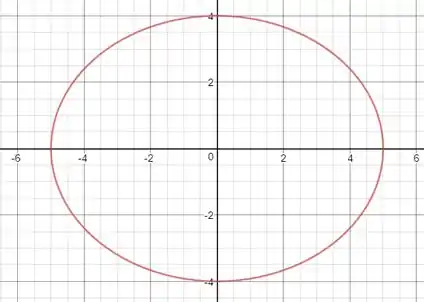
Passo 3
b)
O passo a passo é o mesmo do item anterior, começamos escrevendo na forma canônica:
Como o maior denominador está sobre o teremos a elipse do mesmo jeito do caso anterior, ou seja, caso 1:
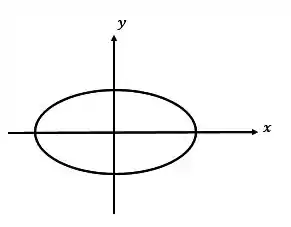
Sendo o maior valor , então:
Utilizando a relação :
Substituindo esses valores a seguir:
Subsituindo, temos:
Esboçando:
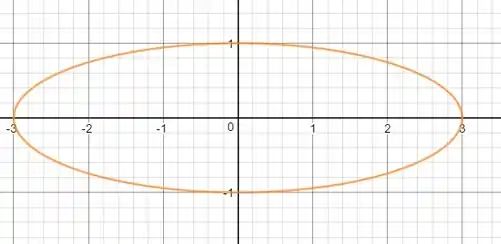
Passo 4
c)
Colocando na forma canônica:
Agora, o maior valor do denominador está dividindo o . Isso indica que estamos no CASO 2, assim nossa elipse terá o seguinte formato:
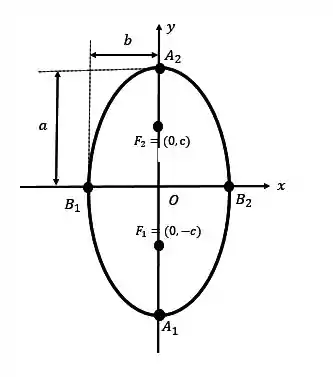
Sabendo que nossa elipse é assim, sabemos que nossos focos e vértices, serão:
Para determina-los precisamos calcular e .
Para encontrar esses valores continuamos a fazer o mesmo procedimento. Assim, o valor de é sempre referente ao maior denominador que é , então:
Usando a relação que é válida para qualquer elipse, temos:
Agora, podemos achar focos, vértices e a excentricidade:
Esboçando:
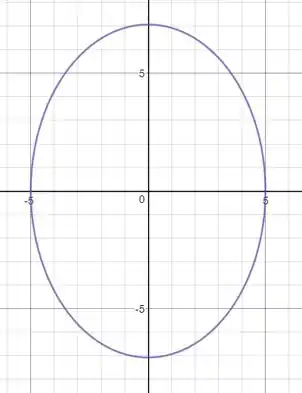
Passo 5
Ufa!! Só falta mais uma!! Uhuuulll
d)
Colocando na forma canônica:
O maior valor do denominador está devidindo o , logo estamos no CASO 1:
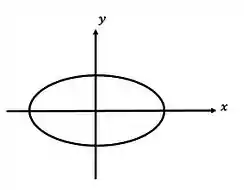
Então, nossos valores de e são:
Tendo os focos, vértices e excentricidade em função de e , temos:
Substituindo:
Para finalizar falta esboçar!!
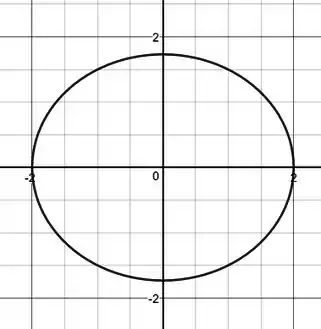
Terminamooossss!!!

Resposta
a)
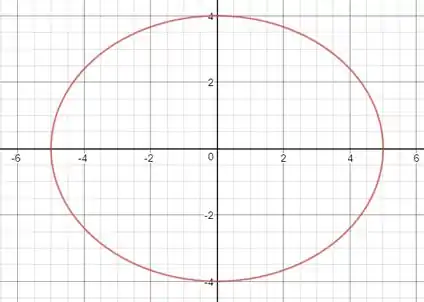
b)
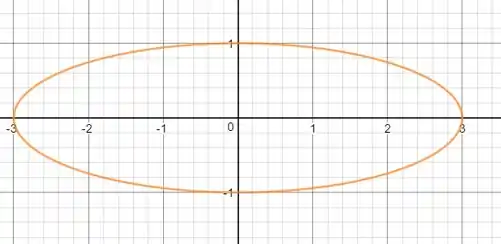
c)
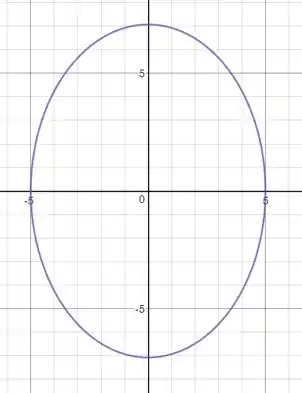
d)
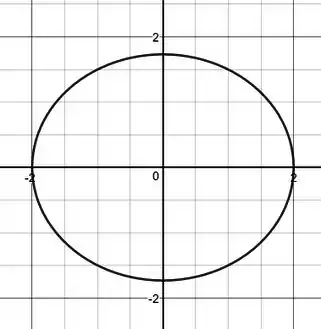
Exercício Resolvido #2
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 237-11.
Uma elipse, cujo eixo maior é paralelo ao eixo dos , tem centro , excentricidade e eixo menor de medida . Qual a equação desta elipse?
Passo 1
Esse exercício é o inverso do que fizemos antes, ou seja, agora temos vários dados sobre a elipse e queremos determinar sua equação.
Dados:
- Eixo maior é paralelo ao eixo dos
- Centro
- Excentricidade
- Eixo menor de medida , ou seja,
Passo 2
Vamos agora utilizar os dados que tiramos do problema para achar a equação da elipse. Primeiro, em qual dos 3 casos estamos?
Bem, para verificar isso vamos olhar para o centro , nosso centro não está na origem , logo é uma elipse transladada. Estamos no caso 3. Assim, teremos uma das equações abaixo.
Qual delas se encaixa no nosso problema?
Bem, como o enunciado nos diz que o eixo maior é paralelo ao eixo dos , então a equação da nossa elipse tem o seguinte jeitão:
Agora, precisamos encontrar o valor dos parâmetros e . O valor de nós conseguimos saber por meio da informação de que o eixo menor mede , então:
O valor de , achamos pela excentricidade:
Sabendo a relação entre e e a relação , achamos :
Bom, e já achamos, mas e e ?
Para achar esses valoresvamos utilizar a última informação que temos que é referente ao centro da elipse estar em , numa translação, o centro está em:
Portanto,
Passo 3
Agora sim, que temostodos os valores, basta substituirmos na expressão . Sendo:
Teremos:
Arrumando:
Resposta
Exercício Resolvido #3
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 239-12.
Determinar o centro, os vértices, os focos e a excentricidade da elipse de equação:
Passo 1
Uhuull!! Mais um problema com elipses!!! Mas, esse é um pouco diferente do que vínhamos fazendo. Precisamos colocar primeiro nossa equação na forma canônica da elipse para então retirarmos as informações que precisamos, que são: centro, vértices, focos e excentricidade.
Passo 2
Para começar, vamos completar quadrados para deixar a expressão na forma reduzida ou canônica da elipse:
Dividindo tudo por :
Pronto!! Chegamos na forma canônica!! Mas, estamos no CASO 3, translação!!
Passo 3
Vamos seguir nossa receita de bolo!! Agora, que já temos a expressão na forma reduzida, vamos passar para o sistema e retirar os dados.
Para passar para o sistema vamos considerar:
Substituindo essas relações, teremos:
Passo 4
Analisando a expressão, percebemos que o maior denominador está sobre o , então isso significa que nosso eixo maior está sobre o eixo , assim estamos no caso 1.
Então, temos que:
E como na elipse temos a relação
Com esses valores conseguimos determinar o que precisamos no sistema . Temos que:
E que a excentricidade vale .
Substituindo os valores de e , temos no sistema :
Passo 5
Para finalizarmos nosso exercício precisamos fazer o último passo da receita, ou seja, passar do sistema para . Para isso, vamos usar as relações:
Fazendo as mudanças teremos:
Fazendo a mesma mudança para os demais vértices, temos:
Para fazemos o mesmo procedimento:
A excentricidade como não depende de então ela não muda
Agora sim, terminamos!!!
