Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Espaços Vetoriais

Ver Todos os Exercícios

Teoria

Opa! Bora aprender o que é um Espaço vetorial e como provar que um conjunto é um espaço vetorial de uma vez por todas?

O que é um Espaço Vetorial?

Um espaço vetorial é definido como:

  • Um conjunto não vazio;
  • Uma soma, tal que
  • Uma multiplicação por um escalar real, tal que

-Hãam? 😖

Essa definição assusta mesmo, mas calma, a gente vai explicar com calma…com exemplos e tudo vai ficar bem claro! Pra começar com o pé direito, dá uma conferida nesse vídeo super completo que o Responde Aí preparou pra você 👇 🧡

📢 Clique para ver mais:

Axiomas do Espaço Vetorial

Pra um conjunto de números ser um espaço vetorial, ele tem que obedecer alguns requisitos que a gente chama de axiomas!

Mas antes de qualquer coisa, pra um conjunto ser um espaço vetorial, qualquer operação feita dentro desse conjunto deve resultar em um vetor que também faça parte desse conjunto! Beleza?

1) A soma é comutativa

2) A soma é associativa

3) Elemento neutro da soma

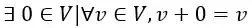
Elemento neutro de soma
Elemento neutro de soma

Ou seja, existe um vetor nesse espaço vetorial, denotado por , cujo resultado da soma com qualquer outro vetor  do espaço é esse outro vetor .

4) Inverso aditivo

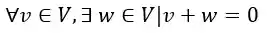
Inverso aditivo
Inverso aditivo

Traduzindo, para todo vetor em , existe um vetor também em , tal que . No universo de operações que conhecemos o inverso aditivo de é o , por exemplo.

5) Associativo

6) Elemento neutro da multiplicação

O elemento neutro é o escalar , cujo resultado da multiplicação dele com qualquer outro vetor do espaço é esse mesmo vetor .

7) Distributividade 1

Axioma de Distributividade 1
Axioma de Distributividade 1

8) Distributividade 2

Axioma de Distributividade 2
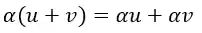
Axioma de Distributividade 2

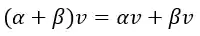
UFAA!! Acabaram os axiomas

Como Provar que um Conjunto é um Espaço Vetorial

Pra a gente provar que um conjunto é um espaço vetorial, a gente tem que ver se ele obedece os 8 axiomas que vimos acima! Por exemplo, considere o conjunto definido por , vamos ver se ele é ou não um espaço vetorial:

Pra começar, vamos fazer uma operação de soma e ver se o vetor resultante pertence a esse conjunto:

Opaa, no vetor resultante temos , então esse vetor não pertence ao conjunto , logo esse conjunto não é um espaço vetorial! Nesse caso podemos parar por aqui, não precisamos conferir todos os axiomas!

Fechou! Agora vamos praticar com exercícios?

Como Provar que um Conjunto é um Espaço Vetorial

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 2ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 85 – Fix. 3.4

O elemento neutro para soma do espaço vetorial das funções reais é o(a):

a Número zero

b Função identidade

c Função identicamente nula

d Conjunto vazio

Passo 1

Como ele não falou nada, devemos usar as operações usuais. Beleza, vamos letra por letra:

a O número zero não pode ser porque ele nem sequer faz parte do espaço vetorial das funções reais. Ele é um número, não uma função!

Passo 2

b A função identidade é aquela que leva um elemento nele mesmo:

f x = x

Se somarmos uma função arbitrária h ( x ) com essa função f ( x ) , teríamos:

h x + f x = h x + x

Logo, essa também não é a certa.

Passo 3

c A função identicamente nula é aquela que leva qualquer elemento em zero:

f x = 0

Se somarmos uma função arbitrária h ( x ) com essa função f ( x ) , teríamos:

h x + f x = h x + 0 = h ( x )

Opa, obtivemos h ( x ) na resposta! Então essa é a certa!

Passo 4

d Essa não faz sentido nenhum, como somaríamos uma função à um conjunto? Eliminada.

Resposta

Função Identicamente Nula.

Exercício Resolvido #2

Elaboração Própria

Dado o espaço vetorial ( V , ∓ , ∸ ) , foram definidas operações de soma e multiplicação por escalar, respectivamente:

1,1 , a ∓ 1,1 , b = 1,1 , a + b ,   a , b ∈ R

α ∸ 1,1 , b = 1,1 , α b ,   α , b ∈ R

Dentre as opções abaixo, marque a alternativa verdadeira:

a O elemento neutro da soma é o vetor 0,0 , 0

b O espaço vetorial V não possui inverso aditivo

c O elemento neutro da soma é 1,1 , 0

d O elemento neutro da multiplicação é α = 0 , pois 0 ⋅ 1,1 , a = ( 1,1 , 0 )

Passo 1

a Bom, nesse caso, podemos ver que ( 0,0 , 0 ) não está definido para o espaço vetorial!

Parando para observar a cara do espaço vetorial V   vemos que ele realiza somas e multiplicações com vetores que possuem o algarismo 1 nas duas primeiras coordenadas, então para pertencer a esse espaço vetorial o vetor tem que ser desse tipo:

( 1,1 , a )   c o m     a   ϵ   R

Assim, como ( 0,0 , 0 ) não pertence a V não é possível efetuar nenhuma operação com ele. Logo, a afirmativa é FALSA.

Passo 2

b Bom, o inverso aditivo é o número negativo que somado com o outro gera o elemento neutro da soma.

Acontece que TODO espaço vetorial possui um inverso aditivo. Se o conjunto de vetores não tivesse a propriedade do inverso aditivo não seria um espaço vetorial.

Mas como foi afirmado que V é um espaço vetorial então ele possui inverso aditivo, logo a afirmativa é FALSA.

Passo 3

c Bom, o elemento neutro seria o vetor que pertence a V que somado com outro resulta nesse outro:

u + 0 = u

Vamos pegar um vetor aleatório que pertença a V e verificar se o vetor ( 1,1 , 0 ) cumpre a função do elemento neutro da soma, beleza?!

Se pegarmos o vetor ( 1,1 , 1 ) , quem seria o elemento neutro?

1,1 , 1 + 1,1 , b = 1,1 , 1 ⇒

1,1 , 1 + b = 1,1 , 1 ⇒

1 + b = 1 ⇒ b = 0

Assim, o elemento neutro é de fato o ( 1,1 , 0 ) e então a afirmativa é VERDADEIRA.

Passo 4

d O elemento neutro da multiplicação seria um número real α   , tal que quando multiplicado com um vetor de V o resultado seria o próprio vetor. Assim,

α ⋅ u = u

Já nessa letra (d), temos:

α = 0 , pois 0 ⋅ 1,1 , a = ( 1,1 , 0 )

Ou seja, ao multiplicarmos um vetor de V obtemos outro vetor diferente do original. Nessa letra acontece isso:

α ⋅ u = v ,   v ≠ u

Então a afirmativa é FALSA.

Resposta

Letra c .

Exercício Resolvido #3

Elaboração Própria

Sobre os conjuntos:

A = { p x = a + b x + c x 2 ∈ P 2 | a + b = 2 }

W = { p ∈ P 2 | a = b = 1 }

E sabendo que W é munido das operações:

1 + x + c 1 x 2 ∔ 1 + x + c 2 x 2 = 1 + x + c 1 2 + c 2 x 2

λ * 1 + x + c x 2 = 1 + x + λ c x 2

  1. Se p 1 , p 2 ∈ A , então p 1 + p 2 ∈ A
  2. W é um espaço vetorial

É correto afirmar sobre as afirmações acima que:

a I e II são verdadeiras

b I é verdadeira e II é falsa

c I e II são falsas

d I é falsa e II é verdadeira

Passo 1

Afirmativa I

Como não se falou nada a respeito das operações de A , iremos utilizar as usuais, beleza?! Vamos usar dois polinômios de W :

p 1 x = a 1 + b 1 x + c 1 x 2

p 2 x = a 2 + b 2 x + c 2 x 2

Somando esses polinômios:

p 1 x + p 2 x = a + b x + c x 2 = a 1 + a 2 + b 1 + b 2 x + c 1 + c 2 x 2

Agora precisamos testar a condição do conjunto, precisamos que a + b = 2 , então:

a 1 + a 2 + b 1 + b 2 = 2

Podemos reordenar essa soma:

a 1 + a 2 + b 1 + b 2 = 2

a 1 + b 1 + a 2 + b 2 = 2

Como p 1 x   e   p 2 x pertencem a A sabemos que a 1 + b 1 = 2 . Então:

a 1 + b 1 + a 2 + b 2 = 2

2 + 2 = 2

4 = 2

Bom, então a afirmativa é falsa, pois 4 ≠ 2 .

Passo 2

Afirmativa II

Olhando as operações de soma e produto por escalar definidas, vemos que ambas resultam em vetores do tipo:

1 + x + c x 2

Portanto, para saber se W é um espaço vetorial devemos testar os axiomas, show de bola?!

1. Vamos tentar provar se a soma é comutativa. Vamos pegar dois polinômios de W :

1 + x + c 1 x 2 e 1 + x + c 2 x 2

Se os dois forem comutativas então, temos que:

1 + x + c 1 x 2 ∔ 1 + x + c 2 x 2 = 1 + x + c 2 x 2 ∔ 1 + x + c 1 x 2

Agora precisamos aplicar exatamente a operação de W definida no enunciado. Nele dizia que:

1 + x + c 1 x 2 ∔ 1 + x + c 2 x 2 = 1 + x + c 1 2 + c 2 x 2

Então, agora desenvolvendo os dois lados da equação que encontramos respeitando a operação, temos:

1 + x + c 1 x 2 ∔ 1 + x + c 2 x 2 = 1 + x + c 2 x 2 ∔ 1 + x + c 1 x 2

1 + x + c 1 2 + c 2 x 2 = 1 + x + c 2 2 + c 1 x 2

O que implica

c 1 2 + c 2 = c 2 2 + c 1

O que claramente não é verdade para todo c 1 e c 2 reais!

Portanto, a afirmativa é falsa!

Resposta

Letra c

Exercícios de Livros Relacionados

Verifique se são espaços vetoriais os seguintes conjuntos:a) O R 2 com a adição usual e a multiplicação por escalar definida por α x , y = α x , 0 . b) O R 2 com x 1 , y 1 + x 2 , y 2 = ( x 1 + 2 x 2
Sejam X um conjunto não vazio e V um espaço vetorial. Mostre que, com as definições naturais de soma e multiplicação por escalar de funções, o conjunto das funções de X em V , F (X; V ), é um espaço v
Nos exercícios 5-6, em cada parte esboce, com ponto incial na origem, o vetor determinado pelos dois pontos dados.6 (a) P1(-1,0,2), P2(0,-1,0)
34 Seja P o ponto 1 ,3 ,7 . Se o ponto 4 ,0 ,- 6 for o ponto médio do segmento de reta que liga P e Q, quem é Q?
O problema apresenta um conjunto com as operações de adição e multiplicação por escalar nele definida. Verificar se é um espaço vetorial, e se não for, cite os axiomas que não se verificam. A = 0 a b