Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Soma da Dimensão de Subespaços

Ver Todos os Exercícios

Teoria

Soma Direta

Lembram daquele exemplo da soma de uma reta com um plano no R 3 ? Esse aqui oh:

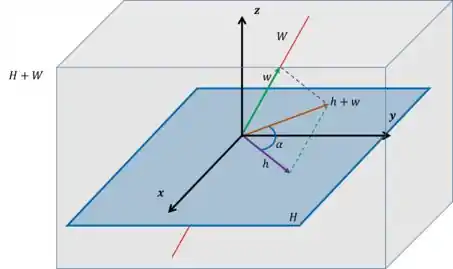
Perceba que a interseção da reta W com o plano H acontece apenas na origem. Quando isso acontece temos uma nomenclatura especial:

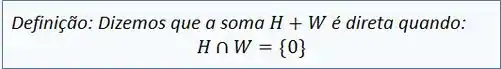
Notação: H ⊕ W

No exemplo anterior, R 3 = H ⊕ W . Mas cuidado!! A definição acima fala quando uma SOMA é direta. Se por exemplo quisermos definir que um espaço E , no caso o R 3 , é soma direta de dois subespaços H ,   W escreveríamos:

Então, podemos dizer que a soma H + W é direta, e que o R 3 é soma direta de H e W .

Dimensão de Subespaços

Ainda referente ao exemplo acima, vimos que a dimensão de H + W era a dimensão de H mais a dimensão de W que no caso dava 3 . Sendo assim, a soma deles gerava o R 3 . Mas e se pegássemos dois planos no R 3 ?

Π 1 = x , y , z ∈ R 3 z - y = 0 }

Π 2 = x , y , z ∈ R 3 z - x = 0 }

Podemos ver que os geradores de Π 1 são:

x , y , y = x 1,0 , 0 + y ( 0,1 , 1 )

E que os de Π 2 são:

x , y , x = x 1,0 , 1 + y ( 0,1 , 0 )

Se pegarmos a soma Π 1 + Π 2 temos que seus geradores são:

s p a n 1,0 , 0 , 0,1 , 1 , 1,0 , 1 , 0,1 , 0

Com um olhar descuidado pode-se dizer que a dimensão da soma desses planos é 4 . Mas como somos muito safos sabemos que não é bem assim. Faltou verificarmos se todos os geradores são L I !

De fato não são, pois é impossível ter 4 vetores L I no R 3 . Logo, basta verificar qual é C L do outro. Ao verificar, vemos que a dimensão do conjunto é 3 .

Po, mas fazer isso toda vez é muito trabalhoso! É verdade, por isso vou te ensinar um outro jeito mais prático de calcular a dimensão de soma de subespaços!

Diferente do nosso primeiro exemplo lá em cima, desta vez os conjuntos em questão possuem uma reta como interseção! (Logo, a soma deles não é direta pois Π 1 ∩ Π 2 ≠ { 0 } !)

Vamos verificar a interseção deste:

z - y = 0 ⇒ z = y z - x = 0 ⇒ z = x

Disso tiramos que:

x = y = z

Logo a interseção dos dois é formada pelo vetor:

x , x , x = x ( 1,1 , 1 )

Assim sendo, podemos ver que a interseção é uma reta, gerada pelo vetor acima, e, portanto, sua dimensão é 1 . Isso já era esperado, pois a interseção de dois planos no R 3 (não-coincidentes) é sempre uma reta!

Agora saca o seguinte: sabemos que a dimensão de cada um dos planos é 2 e que a interseção deles gera uma reta de dimensão 1 . Então,

2 + 2 - 1 = 3

que é exatamente a dimensão da soma dos planos. Se fossem 2 planos iguais, a interseção seria ele próprio e teria dimensão 2 , logo:

2 + 2 - 2 = 2

E de fato a soma de dois planos iguais tem que ser o próprio plano, então deve ter dimensão 2 !

Voltando no exemplo lá de cima, vimos que a dimensão da soma era exatamente a soma das dimensões da reta e do plano. Como a interseção era apenas a origem, sua dimensão é nula.

Equacionando, temos:

1 + 2 - 0 = 3

Percebeu o padrão? Isto não é por acaso! Podemos achar a dimensão da soma facilmente, somando as dimensões de cada um dos conjuntos e diminuindo a dimensão da interseção deles!

Com isso chegamos ao teorema:

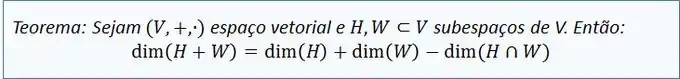
Dimensão de Subespaços

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Sabendo que

H = x , y , z , w ∈ R 4   t 1,0 , 1,0 + s 1,1 , 1,1 , ∀ t , s ∈ R }

S = x , y , z , w ∈ R 4   r 0,1 , 0,1 , ∀ r ∈ R }

Sem fazer muitas contas, qual d i m ⁡ ( H ∩ S ) ?

Passo 1

Bom, vamos usar aquela fórmula linda pra ajudar a gente:

dim ⁡ H + S = dim ⁡ H + dim ⁡ S - dim ⁡ H ∩ S

Vamos achar os geradores de H + S , que é muito mais fácil!

H + S = s p a n 1,0 , 1,0 , 1,1 , 1,1 , 0,1 , 0,1

Este conjunto novo formado por esses três vetores é L D , pois ( 1 , 1,1 , 1 ) é a soma dos outros dois.

Passo 2

Assim, basta eliminá-lo e o conjunto torna-se L I e, portanto, dim ⁡ H + S = 2 .

Sabendo que dim ⁡ H = 2 e dim ⁡ S = 1 , basta usar o teorema e aplicar a fórmula!

dim ⁡ H + S = dim ⁡ H + dim ⁡ S - dim ⁡ H ∩ S

2 = 2 + 1 - dim ⁡ H ∩ S

dim ⁡ H ∩ S = 1

Resposta

dim ⁡ H ∩ S = 1

Exercício Resolvido #2

Elaboração Própria

Sendo:

H = A ∈ M 2 × 2 a 11 = 2 a 22 }

S = B ∈ M 2 × 2 a 12 = 0 }

Calcule uma base para H ∩ S , d i m ⁡ ( H ∩ S ) e d i m ⁡ ( H + S ) .

Passo 1

Neste caso, é mais prático achar a interseção. Para definirmos quais serão seus elementos, e depois uma base, precisamos que estes elementos satisfaçam as duas condições de H e S ao mesmo tempo. Portanto, seria uma matriz 2 × 2 do tipo:

2 d 0 c d = c 0 0 1 0 + d 2 0 0 1

Assim, uma possível base α para H ∩ S é α = 0 0 1 0 , 2 0 0 1 e dim ⁡ H ∩ S = 2 .

Passo 2

Agora, vamos achar uma base para H e S e daí calcular suas dimensões.

Para H temos que

2 d b c d = b 0 1 0 0 +   c 0 0 1 0 + d 2 0 0 1

e dim ⁡ H = 3 .

Para S temos

a 0 c d = a 1 0 0 0 + c 0 0 1 0 + d 0 0 0 1

e dim ⁡ S = 3 .

Passo 3

Assim, usando a fórmula da dimensão da soma temos:

dim ⁡ H + S = dim ⁡ H + dim ⁡ S - dim ⁡ H ∩ S

dim ⁡ H + S = 3 + 3 - 2 = 4

Resposta

α = 0 0 1 0 , 2 0 0 1

dim ⁡ H ∩ S = 2

dim ⁡ H + S = 4

Exercício Resolvido #3

Elaboração Própria

Sendo

H = x , y , z ∈ R 3 x + y - z = 0 }

S = x , y , z ∈ R 3 t 1,1 , 0 , ∀ t ∈ R }

Verifique que H ⊕ S = R 3 .

Passo 1

O problema pede para verificar que a soma direta entre H e S gera o R 3 inteiro. Isso quer dizer que H ∩ S = { 0 } e H + S = R 3 .

Vamos verificar primeiro se a interseção deles é zero de fato.

Passo 2

Para ver se a interseção é realmente zero, podemos verificar se dim ⁡ H ∩ S = 0 , pois acontece se, e somente se, H ∩ S = { 0 } .

dim ⁡ H + S = dim ⁡ H + dim ⁡ S - d i m ⁡ ( H ∩ S )

Para isso, precisamos saber quais são os geradores de H e de H + S .

Passo 3

Para achar os geradores de H , basta entender a condição dada. Assim, podemos vê-la de outro modo:

z = x + y

Portanto, H é formado pelos vetores do R 3 que possui a última coordenada igual a x + y .

x , y , x + y = x 1,0 , 1 + y ( 0,1 , 1 )

Assim é facinho de ver que H = s p a n { 1,0 , 1 , 0,1 , 1 } e, olhando para os zeros nas coordenadas, vemos que eles são L I . Portanto, dim ⁡ H = 2 .

Passo 4

Para achar os geradores de H + S , basta juntar os geradores dos dois:

H + S = s p a n { 1,0 , 1 , 0,1 , 1 , 1,1 , 0 }

De novo, olhando para os zeros, vemos rapidamente que os vetores são L I e, portanto, dim ⁡ H + S = 3 .

Passo 5

O conjunto S possui apenas um gerador, que não é o vetor nulo, portanto dim ⁡ S = 1 .

Aplicando na fórmula da dimensão:

dim ⁡ H + S = dim ⁡ H + dim ⁡ S - dim ⁡ H ∩ S

3 = 2 + 1 - dim ⁡ H ∩ S

dim ⁡ H ∩ S = 0

Como a dimensão da interseção entre os dois conjuntos é zero, temos que a interseção também é nula. E como a soma é formada por 3 vetores L I , sabemos que o s p a n deles gera o R 3 . Logo, H ⊕ S = R 3 .

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Sejam U e V espaços vetoriais sobre R de dimensões m e n , respectivamente. Considere o espaço vetorial U × V cuja adição é dada por u 1 , v 1 + u 2 , v 2 = u 1 + u 2 , v 1 + v 2 E a multiplicação por
Sendo W o sub-espaço do exercício 1 e U o sub-espaço do R 4 gerado por 1 ,2 ,1 ,3 e ( 3 ,1 ,- 1 ,4 ) , determinar uma base e a dimensão de U + W e de U ∩ W .
Suponha que { u 1 , … ,u n } é uma base de um espaço vetorial. Mostrar que { u 1 ,u 1 + u 2 , … ,u 1 + u 2 + … + u n } também é uma base desse espaço.
Determinar a dimensão dos seguintes subespaços de M n ( R ) :Subespaço da matrizes simétricas;Subespaço das matrizes antissimétricas.Subespaço das matrizes A tais que A = 2 A t .Subespaço das matrizes
No espaço vetorial R 3 consideremos os seguintes sub-espaços: U = x ,y ,z x = 0 , V = x ,y ,z y - 2 z = 0e W = 1 ,1 ,0 ,0 ,0 ,2 . Determinar uma base e a dimensão de cada um dos seguintes sub-espaços: