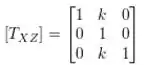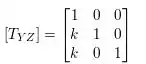Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.11 - Ex. 23
Em , o cisalhamento de fator na direção é a transformação matricial que aplica cada ponto paralelamente ao plano no novo ponto .
- Encontre a matriz canônica do cisalhamento de fator na direção .
- Como você definiria o cisalhamento de fator na direção e o cisalhamento de fator na direção ? Encontre as matrizes canônicas dessas transformações matriciais.
Passo 1
-
Como feito no exercício dessa mesma seção, podemos separar a matriz de transformação em pequenas matrizes elementares tal que:
Sendo , nossas matrizes elementares, organizando pros nossos planos temos:
Que resulta na nossa matriz de transformação de cisalhamento no plano , que é:
Passo 2
Seguindo a mesma lógica do item passado temos:
Por fim:
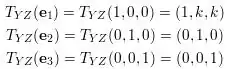
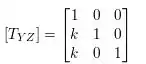
Assim encontramos nossas matrizes de cisalhamento nos 3 planos base do
Resposta
Exercícios de Livros Relacionados
Num dado dia, a qualidade do ar numa certa cidade é boa ou má. Os registros mostram que quando a qualidade do ar é boa num dado dia, então existe uma chance de 95% de que venha a ser boa no próximo di
Num certo instante de tempo inicial, havia 100.000 habitantes numa certa cidade e 25.00 habitantes nos arredores da cidade. A Comissão de Planejamento Regional detectou que, a cada ano, 5% da populaçã
Em cada parte, encontre a matriz canônica do operador T definido pela fórmula.(a) Tx 1 ,x 2 = ( 2 x 1 - x 2 ,x 1 + x 2 ) (b)Tx 1 ,x 2 = x 1 ,x 2 (c) Tx 1 ,x 2 ,x 3 = ( x 1 + 2 x 2 + x 3 ,x 1 + 5 x 2 ,
Em cada parte, determine se T é uma transformação matricial.(a) Tx ,y = ( 2 x ,y ) (b) Tx ,y = ( - y ,x ) (c) Tx ,y = ( 2 x + y ,x - y ) (d) Tx ,y = ( x 2 ,y ) (e) Tx ,y = ( x ,y + 1 )
Em cada parte, encontre a matriz canônica da transformação definida pelas equações.