11. Na figura 2-10, os hexágonos são regulares. Em cada caso, determine a soma dos vetores indicados.
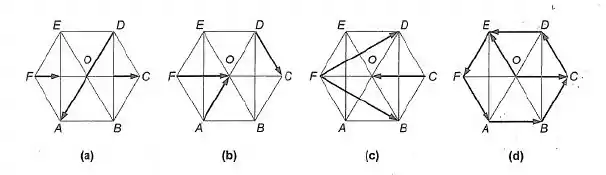
Passo 1
Começaremos com a letra a), vamos lá e faremos por parte
Incialmente vamos fazer a soma do vetor que tem origem em F mais o vetor que tem extremidade em C que dá o vetor.
Agora precisamos somar o vetor com o vetor , que dá o vetor . Então a soma dos vetores na primeira figura é igual a .
Vamos para a letra b)!
O vetor é igual ao vetor . Então temos que fazer a soma:
A soma dos vetores é igual a .
Só que
Então a soma dos vetores da figura é igual a
Passo 2
Vamos para a figura c) agora!
Temos que somar os vetores
Pela regra do paralelogramo, temos que:
A soma do vetores é igual a
Reescrevendo essa soma, temos:
Porém
Então:
A soma dos vetores da figura é igual a !
Passo 3
Para essa última não teremos muito problema, tá vendo os vetores que são os lados do hexágono, a soma de todos esses vetores é zero, já que são consecutivos e formam um polígono!
Então só resta a soma dos vetores , que podemos calcular pela regra do paralelogramo!
Então a soma dos vetores da figura é igual a