12.Dados os pontos distintos A e B, seja . Em cada um dos casos, descreva o conjunto dos valores que deve tomar para que percorra todo o conjunto especificado.
O segmento
A semi-reta de origem que contém
c) A semi-reta de origem que contém A
d) A reta
e) O segmento , que tem como ponto médio.
Passo 1
A questão pede que percorra todo o conjunto especificado.
Para a letra a), temos que deve percorrer o segmento AB, que é assim.
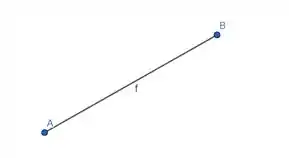
Então tem de ir de até .
Para ser o ponto , temos que ter e para ser ponto
Então, .
Ele vai percorrer todos os pontos de até , portanto está entre e .
Podemos escrever assim:
O intervalo
Passo 2
Para a letra b), temos que deve percorrer a semi-reta de origem A que contém B, que é assim.
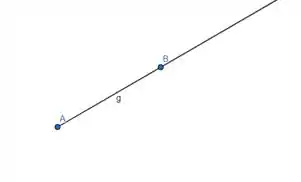
Então tem de ir de até
Para ser o ponto , temos que ter e para ser ponto no infinito precisamos que .
Ele vai percorrer todos os pontos de até , portanto está entre e .
Podemos escrever assim:
O intervalo
Para a letra c), temos que deve percorrer a semi-reta de origem B que contém A , que é assim.
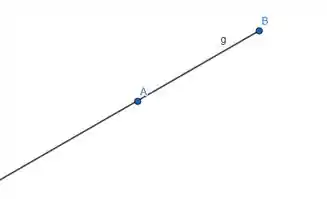
Então tem de ir de até
Para ser o ponto , temos que ter , vimos na letra a) e para ser ponto no precisamos que .
Ele vai percorrer todos os pontos de até , portanto está entre e .
Podemos escrever assim:
O intervalo ] , ]
Passo 3
Para a letra d), temos que deve percorrer a reta AB, que é assim.

Então tem de ir de até .
Para ser ponto no , temos que ter e para ser ponto no . precisamos que .
Ele vai percorrer todos os pontos de até ., portanto está entre e ..
Podemos escrever assim:
O intervalo ] , [
Só que de ] , [ é o conjunto dos Reais.
Para a letra e), temos que deve percorrer o segmento , que tem como ponto médio. É assim:
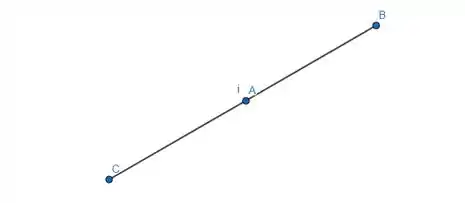
Então tem de ir de até .
Para ser ponto no , devemos descobrir qual o . Se é o ponto médio do segmento , então a relação entra é:
Isolando C, temos:
Só que
Então
Voltando a expressão de
Então .
E para , temos como já calculamos nas letras anteriores.
Então deve percorrer todos os pontos entre e , todos os valores de entre e
O intervalo
Resposta
b)
c) ] , ]
d) O conjunto
e)