Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 8.9 - Ex. 18
18. Uma partícula percorre a trajetória OABO onde O, A e B são pontos (0,0,0), (1,1,0) e (0,1,1) respectivamente (a unidade de comprimento é o metro) com velocidade constante de 1 m/s. Se um campo elétrico induz uma força na partícula dada por:
Calcule o trabalho realizado para percorrer esta trajetória uma vez.
Passo 1
Falaaa... beleza????
Nessa questão vamos usar o produto interno dessa força maluca com o deslocamento pra calcular o trabalho.
Mas ta um pouco estranho isso tudo, né? Então vamos desenvolvendo aos pouquinhos.
Ilustrando um pouco qual vai ser a trajetória todo:
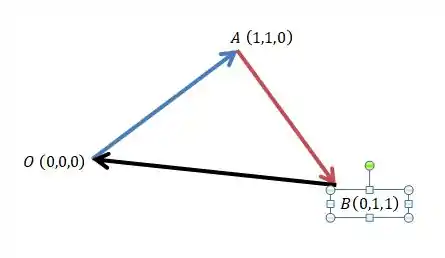
Mas essa força ta muito estranha, né?? Pensa aqui comigo...
Esse deve ser de tempo e como foi dado que a distância entre os pontos é metro e a velocidade é 1 m/s, então a gente consegue ir achar qual o vetor deslocamento em cada segundo, né??
Passo 2
Vamos pegar só o primeiro vetor:
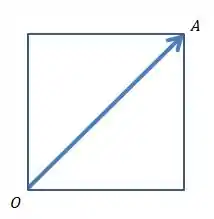
A gente sabe que o tamanho desse vetor é:
Que é maior que 1. Então vamos gastar mais de 1 segundo pra percorrer de A até B, né...
Então vamos precisar dividir a trajetória toda de um metro em um metro... (MISERICÓRDIAA)
Mas continuando... Vai existir um ponto entre e que vai ter a distância vai ser igual a 1 e, consequentemente, o tempo gasto de O a P vai ser 1 segundo:
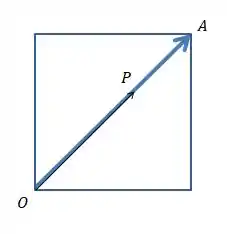
Mas isso daí é um quadrado, então podemos escrever .
E a distância:
Então o ponto é:
E o vetor deslocamento:
Agora “só” falta achar os pontos do resto da trajetória...
Passo 3
Para o segundo 2, vamos achar mais 1 metro:
O restinho que sobrou do vetor AO dá
E confia, mas isso é menor que 1, então pra completar 1, vamos precisar achar um ponto que está entre e .
Repara na figura:
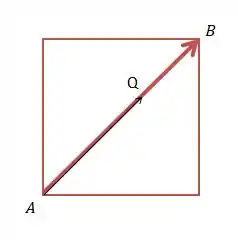
Mas agora quem não varia é o , que é igual a 1 de A até B... e o varia de 0 até 1, então vamos chamar de mesmo. Maas varia de 1 até 0, então vamos chamar de
Então ficamos com e
Igualando:
Daí o ponto Q fica ,
E o vetor:
Passo 4
Será que do ponto Q até o ponto até o ponto B tem mais ou menos 1 metro?
E dá menos que 1, heim...
Então vamos passar pro próximo lado do triângulo...
Vai existir um ponto entre B e O, mas como o x não varia e é igual a zero, o y e o z varia de 1 para 0, então ficamos com:
Maaas:
E o vetor:
Fazendo a distância:
Igualando:
O ponto fica e o vetor:
Passo 5
Vamos ter só mais um ponto, antes de chegar no ponto , de novo...
Mas o x não vai variar e vai ser igual a zero e o y e o z continuam variando igual ao último:
Daí
E o vetor:
E a distância:
Igualando:
E o ponto fica e o vetor (pra 3
E pro último vetor (pra t>4):
Passo 6
Calma calma que não acabou... Falta fazer o monte de produto interno pra achar o trabalho:
Então vamos fazendo aos poucos:
Para
Para
Para :
Para
Para
E, finalmente, fomando isso tudo:
Resposta
Resposta
Ei, a resposta está no passo a passo :)