Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 8.9 - Ex. 22

22. A tabela seguinte lista o número de acidentes em veículos motorizados na Grande São Paulo em alguns anos entre 1960 e 1978.

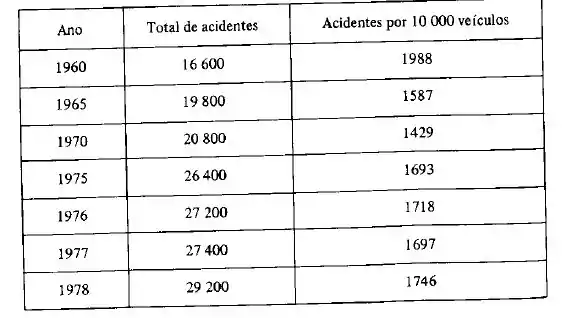
  1. Compute a regressão linear de acidentes no tempo. Use-a para prever o número de acidentes em 1980. Isto recebe o nome de análise de série temporal (i.e. regressão no tempo para prognóstico futuro).
  2. Compute a regressão quadrática do número de acidentes por 10 000 veículos no tempo. Use esta nova regressão para prognosticar o número de acidentes em 1980.
  3. Compare estes resultados. Em qual você está propenso a acreditar e por quê?

Sugestão: utilize os resultados de 8.8

Passo 1

Opaaa... Vamos lá que essa vai ser uma trabalheira danada...

Para a regressão linear vamos usar:

g x = a + b x

Com g 1 x = 1 e g 2 x = x

E o sistema:

< g 1 , g 1 > a + < g 1 , g 2 > b = < g 1 , f > < g 2 , g 1 > a + < g 2 , g 2 > b = < g 2 , f >  

E pra regressão quadrática:

g t = a + b t + c t 2

Com g 1 t = 1 , g 2 t = t e g 3 t = t 2

E o sistema:

< g 1 , g 1 > a + < g 1 , g 2 > b + < g 1 , g 3 > c = < g 1 , f > < g 2 , g 1 > a + < g 2 , g 2 > b + < g 2 , g 3 > c = < g 2 , f > < g 3 , g 1 > a +   < g 3 , g 2 > b + < g 3 , g 3 > c = < g 3 , f >

Haja paciência, heimm... mas vamos lá...

Ahhhh... e vamos dar uma simplificada nesses números aí pra gente sofrer menos, ta bem??

Tipo o 1960 a gente vai chamar de 6 e por aí vai...

Passo 2

  1. Para a regressão linear vamos usar:

    2. g x = a + b x

    Com g 1 x = 1 e g 2 x = x .

    Vamos fazer os produtos internos:

    < g 1 , g 1 >   = 7

    < g 1 , g 2 >   = 50,1

    < g 2 , g 1 >   = 50,1

    < g 2 , g 2 >   = 361,39

    < g 1 , f >   = 167 , 4

    < g 2 , f >   = 1317,36

    E o sistema vai ficar:

    < g 1 , g 1 > a + < g 1 , g 2 > b = < g 1 , f > < g 2 , g 1 > a + < g 2 , g 2 > b = < g 2 , f >  

    Jogando os valores:

    7 a + 50,1 b = 167,4 50,1 a + 361,39 b = 1217,36  

    Resolvendo:

    a = - 25,0025

    b = 6,83469

    Daí a função fica:

    g x = - 25,0025 + 6,83469 x

    Para 1980:

    g 8 = - 25,0025 + 6,83469 8

    g 8 = 2 9,675

    Então 29675 acidentes.

    Passo 3

  2. E pra regressão quadrática:

    3. g t = a + b t + c t 2

    Com g 1 t = 1 , g 2 t = t e g 3 t = t 2

    E o sistema:

    < g 1 , g 1 > a + < g 1 , g 2 > b + < g 1 , g 3 > c = < g 1 , f > < g 2 , g 1 > a + < g 2 , g 2 > b + < g 2 , g 3 > c = < g 2 , f > < g 3 , g 1 > a +   < g 3 , g 2 > b + < g 3 , g 3 > c = < g 3 , f >

    Fazendo os produtos internos:

    < g 1 , g 1 >   = 7

    < g 1 , g 2 >   = 49,8

    < g 1 , g 3 >   = 356,78

    < g 2 , g 1 >   = 49,1

    < g 2 , g 2 >   = 356,78

    < g 2 , g 3 >   = 2572,428

    < g 3 , g 1 >   = 356,78

    < g 3 , g 2 >   = 2572,428

    < g 3 , g 3 >   = 18654,78

    < g 1 , f >   = 12258

    < g 2 , f >   = 86767,6

    < g 3 , f >   = 618870,4

    Daí o sistema:

    7 a + 49,8 b + 356,78 c = 12258 49,8 a + 356,78 b + 2572,428 c = 86767,6 356,78 a +   2572,428 b + 18654,78 c = 618870,4

    Resolvendo o sistema (que obviamente vamos usar algum programa para resolver):

    a = 0,316991

    b = 702,298

    c = - 6 3,6756

    E a função vai ficar:

    g t = 0,316991 + 702,298 t - 63,6756 t 2

    E para 1980: (t=8)

    g 8 = 0,316991 + 702,298 8 - 63,6756 8 2

    g 8 = 1943

    Então 1943 acidentes por 10 000 veículos.

    Passo 4

  3. Agora a gente vai ter que comparar os dois resultados, maaaaaas é um pouco estranho isso, não acha??? Comparar coisas que não estão falando sobre a mesma coisa... Acho que o autor deu uma viajada.

Se liga só que a regressão linear é sobre o número total de acidentes, mas a regressão quadrática é sobre o número de acidentes por 10 000 veículos... E nem tem nenhuma dica de como relacionar esses dados.

Pra saber em qual confiar a gente tem que ter uma fundamentação teórica sobre o que está acontecendo. O nosso caso aqui é dinâmica populacional e não cabe muito representar por regressão quadrática, então a melhor é a regressão linear mesmo.

Resposta

a) g x = - 25,0025 + 6,83469 x

b) g t = 0,316991 + 702,298 t - 63,6756 t 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja W ⊂ R 3 o subespaço gerado por ( 1,0 , 1 ) e ( 1,1 , 0 ) .Considere W ⊥ em relação ao produto interno canônico. Encontre uma base para W ⊥ .A mesma pergunta anterior se W ⊥ é considerado em relaç
Seja T : R 3 → R 3 dada por T x , y , z = ( z , x - y , - z ) e seja W = ker ⁡ T .Encontre uma base ortonormal para W ⊥ (em relação ao produto interno canônico de R 3 ).O mesmo em relação ao produto i
Comprove que as funções definidas nos exemplos do parágrafo 8.1 são produtos internos.
Considere em R 3 o produto internox , y , z , x ' , y ' , z ' = x x ' + 5 y y ' + 2 z z ' Verifique se realmente é um produto interno.A partir da base { 1,0 , 0 , 0,1 , 0 , ( 0,0 , 1 ) } ache uma base
Seja P 2 o espaço das funções polinomiais reais de grau menor ou igual a dois. Definimos em P 2 f , g =∫ - 1 1 f ( t ) g ( t ) d t Considere W o subespaço de P 2 gerado pelos vetores p t = 1 e q t = 1