Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 6.2 - Ex. 18

18. Seja V um espaço com produto interno. Mostre que se w for ortogonal a ambos u 1 e u 2 , então w é ortogonal a k 1 u 1 + k 2 u 2 , quaiquer que sejam os escalares k 1 e k 2 . Interprete esse resultado geometricamente no caso em que V for R 3 com o produto interno euclidiano.

k1u1 k2u2

Passo 1

Vamos primeiro representar os vetores de uma forma genérica:

w = x , y , … ,   n

u 1 = ( x 1 , y 1 , … , n 1 )

u 2 = x 2 , y 2 , … , n 2

Para w ser ortogonal a u 1 :

w ⋅ u 1 = 0

x x 1 + y y 1 + … + n n 1 = 0                           ( i )

Para w ser ortogonal a u 2 :

w ⋅ u 2 = 0

x x 2 + y y 2 + … + n n 2 = 0                           ( i i )

Passo 2

Vamos por partes:

k 1 u 1 = k 1 ( x 1 , y 1 , … , n 1 )

k 1 u 1 = ( k 1 x 1 , k 1 y 1 , … , k 1 n 1 )

k 2 u 2 = k 2 x 2 , y 2 , … , n 2

k 2 u 2 = k 2 x 2 , k 2 y 2 , … , k 2 n 2

Então:

k 1 u 1 + k 2 u 2 = ( k 1 x 1 + k 2 x 2 , k 1 y 1 + k 2 y 2 , … , k 1 n 1 + k 2 n 2 )

Vamos agora fazer o produto interno com w:

w ⋅ k 1 u 1 + k 2 u 2 = x , y , … ,   n ⋅ k 1 x 1 + k 2 x 2 , k 1 y 1 + k 2 y 2 , … , k 1 n 1 + k 2 n 2

= x k 1 x 1 + k 2 x 2 + y k 1 y 1 + k 2 y 2 + … + n k 1 n 1 + k 2 n 2

= k 1 x x 1 + k 2 x x 2 + k 1 y y 1 + k 2 y y 2 + … + k 1 n n 1 + k 2 n n 2

= k 1 x x 1 + y y 1 + … + n n 1 + k 2 ( x x 2 + y y 2 + … + n n 2 )

Agora substituindo ( i ) e i i :

= k 1 0 + k 2 0

= 0

Portanto, é ortogonal, qualquer que sejam k 1 e k 2 .

Passo 3

Uma respresentação beeeem simples no R 3 :

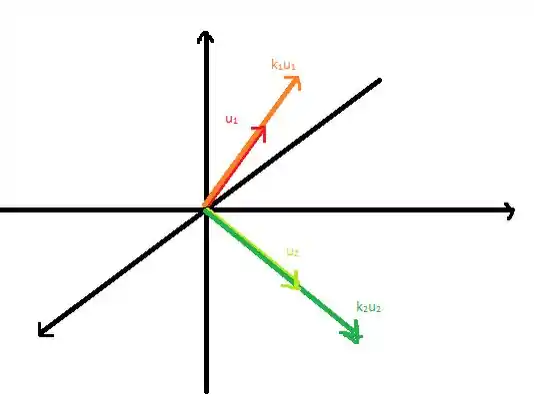
Resposta

Demonstração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

19. Seja V um espaço com produto interno. Mostre que se w for ortogonal a cada um dos vetores u 1 , u 2 , ... , u f , então w é ortogonal a cada vetor em ger{ u 1 , u 2 , ... , u f }.
17. Seja V um espaço com produto interno. Mostre que se u e v forem vetores unitários ortogonais em V , então u - v = 2 .
16. Em cada parte, encontre uma base do complemento ortogonal do subespaço de R n gerado pelos vetores dados.(a) v 1 = ( 1 , - 1,3 ) , v 2 = ( 5 , - 4 , - 4 ) , v 3 = 7 , - 6,2 (b) v 1 = ( 2,0 , - 1 )
21. Seja { w 1 , w 2 , … ,w k } uma base de algum subespaço W de V . Mostre que W ⊥ consiste em todos os vetores de V que são ortogonais a cada um dos vetores da base.
25. Prove: se w 1 , w 2 , … ,w n forem números reais positivos e se u = ( u 1 , u 2 , … , u n ) e v = ( v 1 , v 2 , … , v n ) forem dois vetores quaisquer em R n , então w 1 u 1 v 1 + w 2 u 2 v 2 + …