Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 2.Exercício - Ex. 2

2.Prove que, se vec A B + vec A C = vec B C , então A = B

Passo 1

Inicialmente, desenharemos os vetores vec A B e vec A C . E tentaremos ver a relação entra vec A B , vec A C e vec B C .

Passo 2

Vamos desenhar vec A B e vec A C :

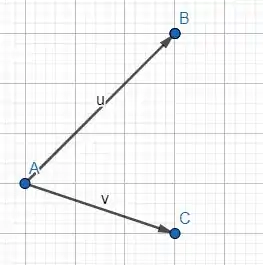
Agora vec B C .

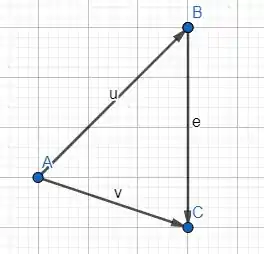
E pela regra do paralelogramo, sabemos que essa diagonal do parelologramo é dada pela diferença entre os vetores vec A C e vec A B .

Então,

vec B C = vec A C - vec A B

Passo 3

Substituindo a relação acima no enunciado, temos:

vec A B + vec A C = vec A C - vec A B

2 vec A B = vec 0

vec A B = vec 0

Se vec A B = vec 0 , então podemos afirmar que A = B .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove a seguinte propriedade do comprimento (ou norma) de um vetor: a )v = 0s e ,es o m e n t es e ,v = 0
Prove a seguinte propriedade do comprimento (ou norma) de um vetor: v + w ≤ v + | w |
Prove que o segmento de reta que une os pontos médios das laterais de um trapézio é paralelo às bases e sua medida é a média aritmética das medidas das bases.
3.1.8 Verifique se os pontos a seguir são colineares, isto é, pertencem a uma mesma reta:(a) A = 5,1 , - 3 , B = 0,3 , 4 e C = 0,3 , - 5