Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Callioli - Álgebra Linear e Aplicações - Parte 2- Ed: 6º - Capítulo 5.2 - Ex. 7

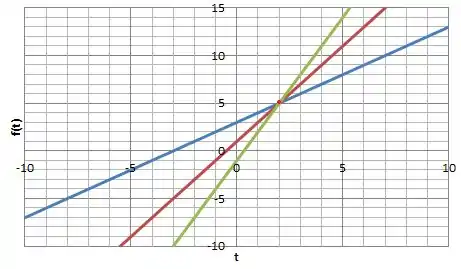
7. Achar todas as funções que estão no núcleo do operador D 2 e cujo valor para t = 2 seja 5. Desenha em um mesmo gráfico algumas dessas funções.

Passo 1

- pra uma função f t estar no núcleo do operador, devemos ter:

L f t = D 2 f t = 0

Passo 2

Vamos agora pensar numa função que satisfaça a condição que ele disse no enunciado:

f 2 = 5

Hmmm... não deu... Vamos então já olhar pro operador e pensar em alguma coisa... Já sei. Concordar que se você derivar a equação de uma reta duas vezes, dá zero?? (e com isso já sabemos que está no núcleo)

Então vamos chamar:

f t = a t + b

Vamos achar o b , com o dado:

f 2 = a 2 + b

5 = 2 a + b

b = 5 - 2 a

E a equação fica:

f t = a t + 5 - 2 a

E é só isso porque ele quer “todas” as funções (até porque não tem como a gente achar o a )

Passo 3

O gráfico é de várias retas, né... vamos atribuir alguns valores para a e montar o gráfico.

- pra a = 1 :

f t = t + 3

- pra a = 3 :

f t = 2 t + 1

- pra a = 3

f t = 3 t - 1

Resposta

f t = a t + 5 - 2 a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache uma solução da equação diferencial que satisfaça a condição dada. d y d x + y tg ⁡ x = sec ⁡ x ; y = 1 quando x = 0 .
Ache a solução completa para a equação diferencial: cos ⁡ x d y d x = 2 + 2 y sen ⁡ x
Ache a solução da equação diferencial que satisfaça a condição dada. x d y d x - 2 y = x 3 + 1 ; y = 1q u a n d ox = 1
Ache a solução completa para a equação diferencial: d y d x = y ln ⁡ y x + ln ⁡ y
Ache a solução completa para a equação diferencial: d y d x = 1 - 2 y 2 sec ⁡ x