Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 33.Problemas - Ex. 6

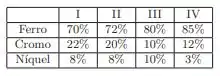
Aço fino e uma liga de ferro, cromo e níquel. Um exemplo é o aço V2A, que contem 74% de ferro, 18% de cromo e 8% de níquel. Na tabela abaixo, tem-se ligas I, II, III e IV, as quais devemos misturar para obter uma tonelada de aço V2A. Quantos quilos de cada uma dessas ligas devemos tomar?

Passo 1

Fala aiii meus lindos tudo blz? espero que sim

Então nessa questão sabe-se que o Aço fino e uma liga de ferro, cromo e níquel. Um exemplo é o aço V2A, que contem 74% de ferro, 18% de cromo e 8% de níquel. Na tabela abaixo, tem-se ligas I, II, III e IV, as quais devemos misturar para obter uma tonelada de aço V2A. e a partir daí ele deseja saber quantos quilos de cada uma dessas ligas devemos tomar?

Precisa fazer esta carinha não que a questão só e extensa, mas ela é linda.

Passo 2

Sabendo que o aço vai V2A contém:

E dado as ligas,

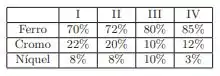
Se acharmos as quantidades em quilos das ligas fica,

Ficando com base da tabela,

A partir daí transformando a última em três teremos um sistema linear de 4 equações valendo

Passo 3

Realizando a equação linear isolando temos,

A partir daí temos,

Fazendo a substituição nos outros denominadores ficamos com,

E por fim no último temos,

Com isso,

Realizando novamente este sistema temos

Ufa, essa foi grandinha rsrs

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

Exercícios de Livros Relacionados

Determine os coeficientes a, b e c da equação do círculo, x 2 + y 2 + a x + b y + c , que passa pelos pontos P 1 = - 2,7 ,P 2 = - 4,5 e P 3 = 4 , - 3 .

Resolva, usando o método de Gauss-Jordan, os seguintes sistemas: x 1 + x 2 + 2 x 3 = 8 - x 1 - 2 x 2 + 3 x 3 = 1 3 x 1 - 7 x 2 + 4 x 3 = 1 0

Os sistemas lineares seguintes possuem a mesma matriz A. Resolva-os usando o método de Gauss-Jordan. b )x 1 - 2 x 2 + x 3 = 2 2 x 1 - 5 x 2 + x 3 = - 1 3 x 1 - 7 x 2 + 2 x 3 = 2

Para cada sistema linear dado, encontre todos os valores de a para os quais o sistema não tem solução, tem solução única e tem infinitas soluções:b)x + y + z = 2 2 x + 3 y + 2 z = 5 2 x + 3 y + a 2 -

Para cada sistema linear dado, encontre todos os valores de a para os quais o sistema não tem solução, tem solução única e tem infinitas soluções:a)x + 2 y - 3 z = 4 3 x - y + 5 z = 2 4 x + y + a 2 -