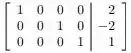Exercícios de Escalonamento - Lista de Exercícios Resolvida

A partir de uma matriz e através da seguinte sequência de operações elementares:

;

;

;

,

Obtém-se a matriz .

Qual dentre as seguintes é a matriz ?

Obs.: Na notação utilizada, indica que a -ésima é substituída por ela mesma acrescida de vezes a -ésima linha e indica a troca das linhas e .

Coloque a matriz abaixo em sua forma escalonada

Determine a forma totalmente escalonada das matrizes abaixo:

Dada a matriz

Sabendo que sua forma escalonada é, quais são os valores de , e ?

Dada a matriz

Dê sua forma escalonada.

Encontre uma matriz escalonada equivalente à seguinte matriz:

Considere as afirmativas abaixo:

I – A matriz não pode ser escalonada, pois não é uma matriz quadrada.

II – Se escalonarmos completamente a matriz , vamos ter como resultado uma matriz identidade de ordem 4

III – Para escalonar uma matriz, temos que encontrar os pivôs e ir realizando operações entre as linhas até encontrarmos uma matriz triangular inferior.

Estão corretas apenas:

a) I

b) II

c) III

d) I e III

e) I e II

f) II e III

Escalona Aí a seguinte matriz:

Sejam matrizes . Considere as afirmativas abaixo:

1- Se tem infinitas soluções, então tem infinitas soluções

2- Se tem solução, então podemos garantir que tem solução para todo .

(A) Apenas I é verdadeira.

(B) Todas são verdadeiras.

(C) Apenas II é verdadeira.

(D) Todas são falsas.

Reduza

à forma escalonada reduzida por linhas sem introduzir quaisquer frações.

Mostre que se , então a forma escalonada reduzida por linhas de

Considere o sistema linear

c) Determine , e de maneira que seja solução do sistema, mas não seja a única.

Determine quantos vetores são linearmente independentes no conjunto abaixo,

Considere as afirmações abaixo:

(I) Seja uma combinação linear de vetores do com coeficientes todos não nulos. Então cada vetor é combinação linear dos demais vetores do conjunto

(II) Seja A uma matriz na forma escalonada. Então uma coluna que não contém pivô é combinação linear das colunas a sua esquerda.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Considere o sistema linear

b) Determine valores para , e de maneira que seja solução do sistema.

Considere as seguintes afirmações:

Um conjunto de vetores é linearmente independente se nenhum deles é múltiplo escalar dos demais.

Se o conjunto é linearmente independente, então o conjunto também é linearmente independente.

Qual das opções abaixo é CORRETA?

A afirmativa é falsa e é verdadeira.

A afirmativa é falsa e é falsa.

A afirmativa é verdadeira e é verdadeira.

A afirmativa é verdadeira e é falsa.

Considere a matriz , cujas linhas são . É dado que uma forma escalonada de é:

Qual dos seguintes conjuntos gera ? (Abaixo, indica o vetor , cuja única entrada não-nula é a -ésima.)

Seja a matriz obtida de através da seguinte sequência de operações elementares:

Qual dentre as seguintes matrizes é a matriz ORIGINAL?

Seja a matriz obtida de através da seguinte sequência de operações elementares:

Qual dentre as seguintes é a matriz original?

Seja . Escolha a alternativa VERDADEIRA

(a) o posto de é

(b) o posto de depende dos valores de e

(c) O posto de é

(d) o posto de é

(e) Não sei

Calcule o determinante da matriz

Se são tais que:

Então é igual a:

Calcule os determinantes da matriz abaixo por escalonamento. Expresse seu cálculo como uma sequência de igualdades entre determinantes e tenha o cuidado de usar os três tipos de operações elementares

A é uma matriz qualquer. Escalonando-se A, aparece uma linha de zeros. Considere as afirmações abaixo:

(I) Pode-se concluir que o conjunto das colunas de A é linearmente dependente.

(II) Pode-se concluir que o conjunto das linhas de A é linearmente dependente.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

A partir de uma matriz e através da seguinte sequência de operações elementares:

;

;

;

,

Obtém-se a matriz .

Qual dentre as seguintes é a matriz ?

Obs.: Na notação utilizada, indica que a -ésima é substituída por ela mesma acrescida de vezes a -ésima linha e indica a troca das linhas e .

Sejam uma matriz e a sua forma escalonada. Considere as seguintes afirmativas:

1. As colunas de são combinações lineares das colunas de .
2. As linhas de são combinações lineares das linhas de .

é falsa, é verdadeira.

e são verdadeiras.

é verdadeira, é falsa.

e são falsas.

O que NÃO podemos afirmar sobre o escalonamento de matrizes reais:

As linhas não nulas da forma escalonada de uma matriz formam um conjunto linearmente independente

Na forma escalonada de uma matriz qualquer, o número de colunas linearmente independentes é igual ao de linhas linearmente independentes

Ao escalonar uma matriz , com , sempre vamos obter pelo menos linhas nulas

Se duas matrizes e têm a mesma matriz na forma escalonada, então necessariamente

Considere as seguintes afirmações:

Se o conjunto é linearmente independente, então o conjunto também é linearmente independente.

Se e são dois conjuntos linearmente dependentes, então podemos ter linearmente independente.

Qual das opções abaixo é CORRETA?

A afirmativa é falsa e é falsa.

A afirmativa é falsa e é verdadeira.

A afirmativa é verdadeira e é verdadeira.

A afirmativa é verdadeira e é falsa.

Assinale uma forma escalonada da matriz:

(A)

(B)

(C)

(D)