Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 29
Adapte ao paraboloide elíptico o método que utilizamos para esboçar o paraboloide hiperbólico.
Passo 1
Vamos acompanhar o mesmo método que o livro usou para esboçar o paraboloide hiperbólico.
A equação do paraboloide elíptico é:
O primeiro passo é descobrir qual é a forma da interseção dessa superfície com cada plano.
Primeiro vamos fazer a interseção com planos paralelos a , nos quais ( é uma constante qualquer):
E essa é a equação de uma elipse, então nos planos paralelos a a superfície é uma elipse:
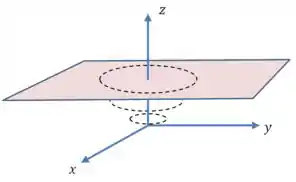
E quanto maior é o valor de , maiores são os eixos dessa elipse!
Passo 2
Bom, olha o que acontece quando calculamos as interseções com os planos paralelos a , ou seja, quando fazemos :
E esse termo é uma constante que podemos chamar de , por exemplo:
Então:
Ou seja, temos uma parábola em , com uma constante que dá a altura da parábola em relação a origem.
E essas parábolas vão se encaixar nas elipses que vimos antes:
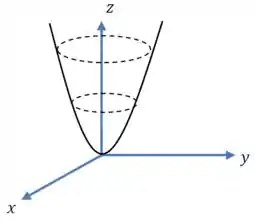
E a exata mesma coisa acontece quando fazemos ! A essa altura já dá pra visualizar como fica a superfície:
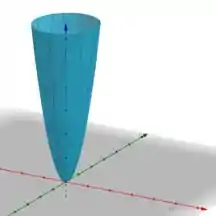
Resposta
Demonstração. Veja os desenhos.