Um agricultor costuma plantar feijão e arroz. Sua propriedade dispõe de 40ha de terra cultivável, mas apenas 20ha podem ser usados para plantar arroz. Ele tem condições de pagar 2400 horas de trabalho no verão e 1380 horas no inverno. Suas culturas apresentam as seguintes características:

Quantos hectares de feijão e quantos de arroz ele deve plantar de modo a maximizar seu lucro? (A área utilizada para plantar cada um dos cereais é a mesma em ambos os plantios.)
Passo 1
Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??
Vamos definir as seguintes variáveis para o nosso problema:
X: quantidade de hectares de feijão a serem plantados.
Y: quantidade de hectares de arroz a serem plantados.
Analisando o contexto do problema temos as seguintes desigualdades:
Além disso, é óbvio que a quantidade de hectares de cada cereal precisa ser maior ou igual a zero, logo: .
Representando cada uma das retas que compõe esse sistema de desigualdades no plano cartesiano, temos a seguinte região:
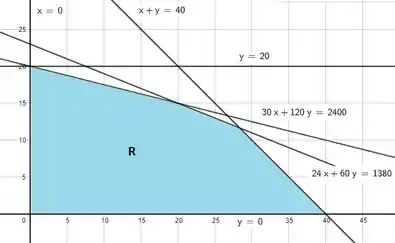
Passo 2
Desejamos agora encontrar nessa região os valores para X e Y que maximizem o lucro, que é dado pela função:
Um método prático de achar o ponto de máximo da função L consiste em calcular L(P) para todo vértice P da nossa região R e ver qual desses valores é o maior.
Observando melhor a região, conseguimos determinar quatro vértices como potenciais candidatos a maximizar o lucro, são eles: A = (0,20), B = (20,15), C = (28.33,11.67) e D = (40,0).
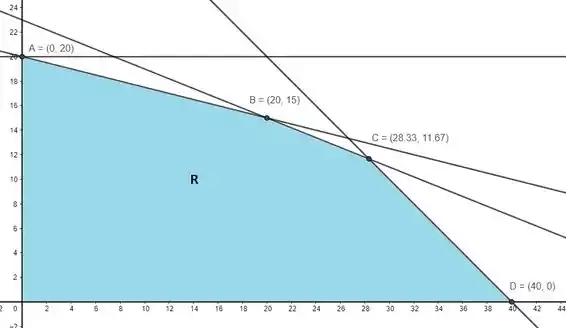
Calculando os Lucros, em A, B, C e D, temos que:
Logo, percebemos que a melhor solução é o ponto B, ou seja, para maximizar os lucros obtidos o agricultor deve plantar 20 hectares de feijão e 15 hectares de arroz.
Note que, nessa solução não é utilizada toda a área cultivável de 40 hectares. Caso o problema proposto condicionasse a resposta ao fato de que era preciso usar toda a área cultivável aí a solução ótima seria o ponto C.
Resposta
O agricultor deve plantar 20 hectares de feijão e 15 hectares de arroz.