Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 4.2 - Ex. 20

O ângulo entre uma reta r que tem vetor diretor V = ( a , b , c ) e um plano π que tem vetor normal N = ( a π , b π , c π ) é definido pelo complementar do ângulo entre uma reta perpendicular ao plano π e a reta r . Mostre que

sin ⁡ ( r , π ) = N ⋅ V N V .

Passo 1

Eaew, belezinha? Bora fazer mais uma?

Vamos começar observando o seguinte esquema:

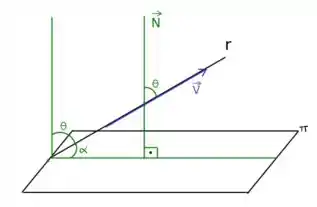
Vamos analisar este esquema com mais calma! Bora lá!

Passo 2

Note que se considerarmos o módulo do produto escalar entre N → e V → , temos que:

N → ⋅ V → = N → V → cos ⁡ ( θ )

Nós temos que:

π 2 = θ + α → θ = π 2 - α

Portanto, temos que:

N → ⋅ V → = N → V → cos ⁡ π 2 - α = N → V → cos ⁡ π 2 - α

Vamos reescrever isso um pouquinho!

Passo 3

Lembrando que:

cos ⁡ A + B = cos ⁡ ( A ) cos ⁡ ( B ) - sin ⁡ A sin ⁡ ( B )

E como, cos ⁡ ( π 2 ) = 0 e sin ⁡ ( π 2 ) = 1 . Temos que:

cos ⁡ ( π 2 - α ) = sin ⁡ ( α )

E portanto, temos que:

N → ⋅ V → = N → V → sin ⁡ ( α )

Finalmente, temos que:

sin ⁡ ( α ) = N → ⋅ V → N → V →

Para garantirmos que as direções dos vetores sejam irrelevantes, é necessário considerar:

sin ⁡ ( α ) = N → ⋅ V → N → V →

Como queríamos demonstrar, te vejo na próxima! Tchauzinho!

Resposta

Ao longo dos passos!

Exercícios de Livros Relacionados

Seja π 1 o plano que passa pelos pontos A = (1, 1, 1), B = (1, 0, 1), C = (1, 1, 0) e π 2 o plano que passa pelos pontos P = (0, 0, 1) e Q = (0, 0, 0) e é paralelo ao vetor i → + j → . Ache o ângulo e
Determine a equação do plano π 1 que passa por A = (10/3, 1, -1), B = (1, 9/2, -1) e C = (1, -1, 5/6).
Dados A = (0, 2, 1), r: X = (0, 2, -2) + t(1, -1, 2), ache os pontos de r que distam 3 de A. A distância do ponto A à reta r é maior, menor ou igual à 3 ? Por que?
Dada a reta r: X = (1, 0, 0) + t(1, 1, 1) e os pontos A = (1, 1, 1) e B = (0, 0, 1), ache o ponto de r equidistante de A e B.
Seja r 1 a reta que passa pelos pontos A = (1, 0, 0) e B = (0, 2, 0) e r 2 a reta: x - 2 = y - 3 2 = z - 4 3 Encontre as equações da reta perpendicular às retas r 1 e r 2 .