Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 4.2 - Ex. 21
A distância entre uma reta que passa por um ponto e tem vetor diretor e um plano é definida como a menor distância entre dois pontos um de e outro de . Se o vetor da reta , , não é ortogonal ao vetor normal do plano , , então a reta e o plano são concorrentes e a distância entre eles é igual à zero, caso contrário a distância é igual de um ponto da reta ao plano . Mostre que
Passo 1
Eaew, belezinha? Vamos começar mais uma!
Aqui o ponto chave é analisar que se não existe ortogonalidade entre o vetor diretor de uma reta e o vetor normal de um plano, a reta cruza o plano necessariamente, e, portanto, a distância é nula nesta condição. Saca só o seguinte esquema:
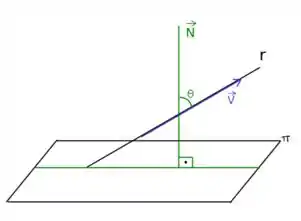
Agora, no entanto, se , temos que a reta é paralela ao plano . O processo para calcular a distância então é feito de outra maneira, saca só!
Passo 2
Vamos lembrar aqui que para calcular a distância entre um ponto e um plano, temos que:
Sejam um ponto que passa pela reta e um plano. A distância de a é dada por
Em que e é um ponto de (isto é, um ponto que satisfaz a equação de ).
Vamos tentar utilizar tudo isso para resolver a questão! Bora lá!
Passo 3
A primeira coisa que podemos fazer é identificar que temos um vetor normal e sua norma é tal que:
Beleza, até aqui tudo bem! Agora, no entanto, precisamos de um ponto que pertença ao plano! Saca só como podemos achar ele!
Passo 4
Se colocarmos , temos que
Portanto, um ponto que pertence ao plano é tal que:
Agora vamos escrever o vetor !!
Passo 5
Temos que:
De forma, que:
Ou seja, temos que:
Resumindo então os resultados, temos que:
A questão é isso, te vejo na próxima!! Tchauzinho!
Resposta
Ao longo dos passos!