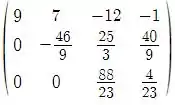Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 33.Problemas - Ex. 15
Aplique o processo de escalonamento a cada um dos sistemas abaixo e, a partir do resultado, identifique em qual dos oito casos da seção anterior o sistema se enquadra.
1)
2)
3)
4)
5)
6)
7)
8) 4
Passo 1
Saudações galerinha, tudo bem?
Vamos começar a resolver mais um exercício, bora lá então!
Inicialmente temos uma questão tem trabalhosa mais com calma, vamos dominar a fera!
Dado o sistema vamos aplicar o escalonamento, beleza!
Vamos começar escrevendo a matriz resultante:
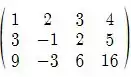
Aplicando , teremos:
Aplicando , e invertendo teremos:
De acordo com a classificação indicada no livro texto esse sistema possui solução
Pronto escalonamento realizado com sucesso, bora pra frente que ainda temos 7 a fazer!
Passo 2
Dado o sistema vamos aplicar o escalonamento, beleza!
Vamos começar escrevendo a matriz resultante:
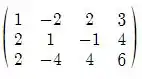
Aplicando , teremos:
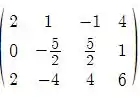
Aplicando , e invertendo teremos:
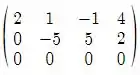
De acordo com a classificação indicada no livro texto esse sistema não possui solução
Pronto escalonamento realizado com sucesso, bora pra frente que ainda temos 6 a fazer!
Passo 3
Dado o sistema vamos aplicar o escalonamento, beleza!
Vamos começar escrevendo a matriz resultante:
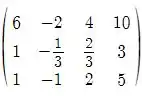
Aplicando , teremos:
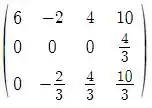
Aplicando , e invertendo teremos:
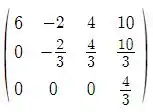
De acordo com a classificação indicada no livro texto esse sistema possui solução
Pronto escalonamento realizado com sucesso, bora pra frente que ainda temos 5 a fazer!
Passo 4
Dado o sistema vamos aplicar o escalonamento, beleza!
Vamos começar escrevendo a matriz resultante:
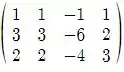
Aplicando , teremos:
Aplicando , teremos:
De acordo com a classificação indicada no livro texto esse sistema possui solução
Pronto escalonamento realizado com sucesso, bora pra frente que ainda temos 4 a fazer!
Passo 5
Dado o sistema vamos aplicar o escalonamento, beleza!
Vamos começar escrevendo a matriz resultante:
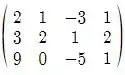
Aplicando , teremos:
Aplicando , teremos:
De acordo com a classificação indicada no livro texto esse sistema não possui solução
Pronto escalonamento realizado com sucesso, bora pra frente que ainda temos 3 a fazer!
Até aí tranquilo?
Calma quase acabando!
Passo 6
Dado o sistema vamos aplicar o escalonamento, beleza!
Vamos começar escrevendo a matriz resultante:
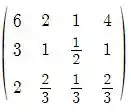
Aplicando , teremos:
Aplicando , teremos:
De acordo com a classificação indicada no livro texto esse sistema possui solução
Pronto escalonamento realizado com sucesso, bora pra frente que ainda temos 2 a fazer!
Passo 7
Quase acabando!
Dado o sistema vamos aplicar o escalonamento, beleza!
Vamos começar escrevendo a matriz resultante:
Aplicando , teremos:
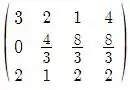
Aplicando , teremos:
De acordo com a classificação indicada no livro texto esse sistema possui solução
Pronto escalonamento realizado com sucesso, bora pra frente que ainda temos 1 a fazer!
Passo 8
Dado o sistema vamos aplicar o escalonamento, beleza!
4
Vamos começar escrevendo a matriz resultante:
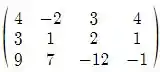
Aplicando , e inverter teremos:
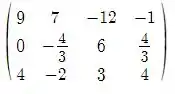
Aplicando , teremos:
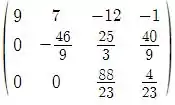
De acordo com a classificação indicada no livro texto esse sistema não possui solução
Pronto escalonamento realizado com sucesso, bora pra frente que ainda temos 1 a fazer!
Ufa!
Acabamos te vejo na próxima questão!
Resposta
1)
2)
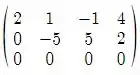
3)
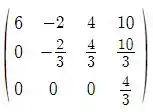
4)
5)
6)
7)
8)
