Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 12.Exercício - Ex. 13a

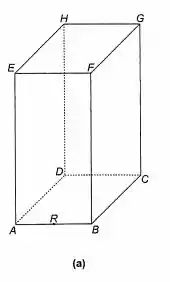
As arestas AB, AD e AE do paralelepípedo retângulo mostrado na Figura 12-6(a) medem, respectivamente 1, 2 e 2. R é ponto médio de AB, e a base G H → ,   G F → ,   G C → é positiva.

(a) Calcule D E → ,   D R → ,   D F → .

Passo 1

Bora lá!

Para calcularmos o produto misto desejado, devemos escrever os três vetores em relação a uma base ortogonal positiva. A base positiva dada é E = G H → ,   G F → ,   G C → . Para obtermos a base ortogonal, precisamos do módulo desses vetores.

Sabemos que:

A B → = 1 ; A D → = 2 ; A E → = 2

Assim, por uma relação de indentidade, temos:

G H → = 1 ; G F → = 2 ; G C → = 2

Passo 2

Seja F = ( p → ,   q → ,   r → ) a nossa base ortonormal positiva. Para obtermos F a partir do passo anterior, fazemos:

p → = G H → G H → = G H →

q → = G F → G F → = G F 2 →

r → = G C → G C → = G C 2 →

Passo 3

Agora, nós precisamos escrever os vetores D E → ,   D R → e D F → em relação a base ortonormal positiva F = p → ,   q → ,   r → . Fazendo isso, temos:

D E → = G F → - G C → = 2 . G F → 2 - 2 . G C → 2 = 2 q → - 2 r → = 0 ,   2 ,   - 2 F

D R → = - 1 2 G H → + G F → = - 1 2 G H → + 2 . G F → 2 = - 1 2 q → + 2 q → = - 1 2 ,   2 ,   0 F

D F → = - G H → + G F → - G C → = - G H → + 2 . G F → 2 - 2 . G C → 2 = - p → + 2 q → - 2 r → = - 1 ,   2 ,   - 2 F

Passo 4

Por fim, para calcularmos o produto misto de D E → ,   D R → e D F → , fazemos:

D E → ,   D R → , D F → = 0 2 - 2 - 1 2 2 0 - 1 2 - 2 = 2 - 4 - 2 = - 4

Portanto o produto misto entre D E → ,   D R → , D F → é - 4 .

Resposta

(a) D E → ,   D R → , D F → = - 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

72. Calcular o valorr de m para que o volume do paralelepípedo determinado pelos vetores v 1 = 2 i - j , v 2 = 6 i + m j - 2 k e v 3 = - 4 i + k seja igual a 10.
71. Sejam os vetores u = 1,1 , 0 , v = 2,0 , 1 , w 1 = 3 u - 2 v ,w 2 = u + 3 v e w 3 = i + j - 2 k . Determinar o volume do paralelepípedo definido por w 1 , w 2 e w 3 .
68. Verificar se são coplanares os pontos:a) A 1,1 , 1 , B - 2 , - 1,3 , C 0,2 , - 1 e D - 1,0 , - 2 b) A 1,0 , 2 , B - 1,0 , 3 , C 2,4 , 1 e D - 1 , - 2 ,2 c) A 2,1 , 3 , B 3,2 , 4 ,C - 1 , - 1 , - 1
74. Dados os pontos A 1 , - 2,3 ,B 2 , - 1 , - 4 , C 0,2 , 0 e D - 1 , m , 1 , determinar o valor de m para que seja de 20 unidade de volume o volume do paralelepípedo determinado pelos vetores A B ,
Qual o volume do cubo determinado pelos vetores i → ,j →ek → ?